之前创建虚拟机时不知道需要多大空间，给了20G，装了ROS相关套件之后磁盘使用率到了90%。

然后在硬盘设置里面调整到了60G，我以为这样就可以了。。。。

too naive。。。还是要手动配置一下，需要安装工具Gparted：

1

sudo apt-get install gparted

然后先抹掉extended和swap两个分区，然后就可以resize主分区了，然后在重新创建那两个分区就好了。

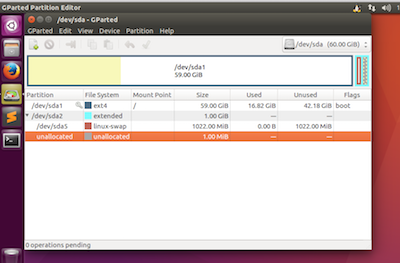
Attention：磁盘只能扩展，不能变小，因此建议逐渐扩展。

SLAM前端主要解决两个问题，一是从不同时刻的传感器输入中识别出同一个地图特征，二是计算每个当前时刻机器人相对该特征的位姿。

vSLAM能够轻松解决前者，LidarSLAM解决后者无压力。本文讨论激光SLAM前端问题1——特征点匹配。目前两大常用思路：scan2scan——ICP，scan2map——CSM。

basic的CSM算法思路如下：从前一帧机器人位姿开始，寻找最优刚性变换，使雷达点在栅格地图中的位置尽量对应于占据度为1的栅格。

为了保持定位信息原有的数位精度，使用双线性插值方法来获取雷达点的地图值(占据度)，而不是使用其所在栅格的地图值来直接对应：

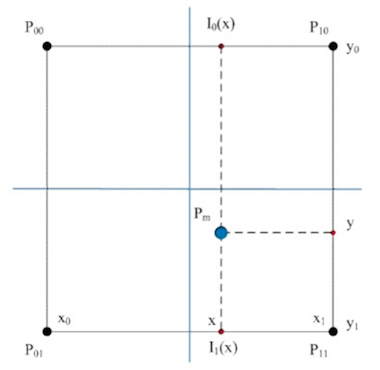
$Pm$是雷达点，$P_{00}, P_{01}, P_{10}, P_{11}$是雷达点邻近的四个栅格中心点。于是得到地图值：

雷达点所在位置的地图值变化梯度：

记当前时刻的已有地图$M$，当前帧共输入$n$个雷达点$S_1, …, S_n$，其对应位置的占据度为$M(S_k)$，最优变换定义为$\xi = (\Delta x, \Delta y, \psi)^T$，则最优问题的最小二乘描述为：

scan2map的鲁棒性更强，但是实时性上打了折扣。对此主要有两个改进措施：一是局部搜索，二是分辨率金字塔。

一、局部搜索

实际计算中会选定一个搜索区间，通常只在上一时刻地图位置的附近，对其中包含的全部可能位姿进行评分。

上式（最小二乘表达式）只包含了雷达端点，考虑到传感器的噪点影响，局部极值影响大。

• 基于模版的匹配：雷达端点及射线所在栅格构成的多边形区域，以此作为局部地图，进行map2map匹配。减少局部极值的影响，提高计算代价，同时考虑到动态目标，会引入新的局部极值。

• LM算法：迭代的方式求解最小二乘的最优解。

• 分支界定算法：基于广度优先搜索的算法，通过对解空间搜索树的分支进行扩展和剪枝，不断调整搜索方向，加快找到全局最优解的速度。界定核心：若当前分支的下界$C_{branch}$小于解空间上界$C_{HB}$，则进行拓展，否则进行裁剪，直至到达叶子结点，即找到最小代价解。

二、多分辨率金字塔

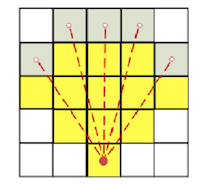
两帧雷达点云的相似区域并不会影响匹配的最终结果，但会参与计算，导致搜索效率降低，需要更多的迭代次数达到收敛。

当地图分辨率较低时，部分地图信息会被忽略，这种高、低分辨率下的差异，有助于对地图中的相似场景进行区分。实际使用中，首先将初始位姿对应的雷达点云与最上层（粗分辨率）的地图进行匹配，计算出当前分辨率下的位姿，并作为初始值进入次一级地图进行匹配，以此类推。

1. 概述

• 经典的SLAM模型由一个运动方程和一个观测方程构成： $$\left\{ \begin{split} & x_k = f(x_{k-1}, u_k) + w_k\\ & z_{k,j} = h(y_i, x_k) + v_{kj} \end{split} \right.$$ 其中，$x_k$表示相机的位姿，可以用变换矩阵或李代数来表示，$y_i$表示路标，也就是图像中的特征点，$w_k$和$v_{kj}$表示噪声项，假设满足零均值的高斯分布。

• 我们希望通过带噪声的观测数据$z$和输入数据$u$推断位姿$x$和地图$y$的概率分布。主要采用两大类方法，一类是滤波方法：基于当前状态来估计下一状态，忽略历史；一类是非线性优化方法，使用所有时刻的数据估计新状态的最优分布。
  • 滤波方法主要分为扩展卡尔曼滤波和粒子滤波两大类。
  • 非线性优化根据实现细节的不同主要分为滑动窗口法和Pose Graph法。

2. 非线性优化

• 非线性优化基于历史，同时也作用于历史，因此把所有待估计的变量放在一个状态变量中：

  $$x = \{x_1, ..., x_N, y_1, ..., y_M\}$$

  在已知观测数据$z$和输入数据$u$的条件下，对机器人的状态估计：

  $$P(x | z,u)$$

  先忽略测量运动的传感器，仅考虑测量方程，根据贝叶斯法则：

  $$P(x|z) = \frac{P(z|x)P(x)}{P(z)} \varpropto P(z|x)P(x)$$
  • 先验概率$P(x)$：先验的概念最好理解，就是一个事件的概率分布。
  • 似然概率$P(z|x)$：已知事件的概率分布，事件中某状态的概率。
  • 后验概率$P(x|z)$：在给定数据条件下，不确定性的条件分布。
  • $Posterior \varpropto Likelihood * Prior$

  求解后验分布比较困难，但是求一个状态最优估计（使得后验概率最大化）是可行的：

  $$x^*_{MAP} = argmaxP(x|z) = argmaxP(z|x)P(x) = argmaxP(z|x)$$

  因为先验概率不知道，所以问题直接转成为求解极大似然估计，问题中的未知数是$x$，直观意义就是：寻找一个最优的状态分布，使其最可能产生当前观测到的数据。

• 假设了噪声项$v_{kj} \thicksim N(0, Q_{k,j})$，所以极大似然概率也服从一个高斯分布：

  $$P(z_{kj}|x_k, y_j) = N(h (y_j, x_i), Q)$$

  求高斯分布的最值通常取负对数处理，最大化变成求最小化：

  $$P(x) = \frac{1}{\sqrt{(2\pi)^Ndet(\Sigma)}} exp\bigg(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\bigg)\\ -ln(P(x) ) = \frac{1}{2}ln\big((2\pi)^Ndet(\Sigma)\big) + \frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)$$

  对数第一项与$x$无关，第二项等价于噪声的平方项。因此可以得到优化问题的目标函数：

  $$e_{k} = x_k - f(x_{k-1}, u_k)\\ e_{kj} = z_{kj} - h(x_k, y_j)\\ J(x) = \Sigma e_k^TR^{-1}_ke_{k} + \Sigma e_{kj}^TQ^{-1}_ke_{kj}\\ x* = argmin_x J(x)$$

  以上的最小二乘问题可以采用各种各样的梯度下降法求解最优解（参考图优化）。

• Bundle Ajustment

  优化问题最终可以表示成$H\Delta x = g$的形式，其对角线上的两个矩阵为稀疏矩阵，且右下角的矩阵维度往往远大于左上角（因为特征点的数目远大于位姿节点）：

  $$H = \begin{bmatrix} B &E\\ E^T & C \end{bmatrix}$$

  一个有效的求解方式称为Schur消元，也叫边缘化Marginalization，主要思路如下：首先求解$C$矩阵的逆矩阵，然后对$H$矩阵进行消元，目标是消去其右上角的$E$矩阵，这样就能够先独立求解相机参数$\Delta x_c$，再利用求得的解来求landmarks参数$\Delta x_p$：

  $$\begin{bmatrix} I &-EC^{-1}\\ 0 & I \end{bmatrix} \begin{bmatrix} B &E\\ E^T & C \end{bmatrix} \begin{bmatrix} \Delta x_c \\ \Delta x_p \end{bmatrix} = \begin{bmatrix} I &-EC^{-1}\\ 0 & I \end{bmatrix} \begin{bmatrix} v \\ w \end{bmatrix} \\ \begin{bmatrix} B - EC^{-1}E^T & 0\\ E^T & C \end{bmatrix}\begin{bmatrix} \Delta x_c \\ \Delta x_p \end{bmatrix} = \begin{bmatrix} v - EC^{-1}w\\ w \end{bmatrix}$$

  因此可以解得$\Delta x_c$：

  $$\begin{bmatrix} B - EC^{-1}E^T \end{bmatrix} \Delta x_c = v - EC^{-1}w$$
  • 这个矩阵称为消元之后的$S$矩阵，它的维度与相机参数的维度一致
  • $S$矩阵的意义是两个相机变量之间是否存在着共同观测点
  • $S$矩阵的稀疏性由实际数据情况决定，因此只能通过普通的矩阵分解的方式来求解

• 核函数

  当误差很大时，二范数增长的很快，为了防止其过大掩盖掉其他的边，可以将其替换成增长没那么快的函数，使得整个优化结果更为稳健，因此又叫鲁棒核函数，常用的核有Huber核、Cauchy核、Tukey核等，Huber核的定义如下：

  $$H(e) = \left\{ \begin{split} & \frac{1}{2} e ^2, \ \ \ |e| \leq \delta\\ & \delta(|e| - \frac{1}{2}\delta), \ \ else \end{split} \right.$$

3. 卡尔曼滤波

滤波思路基于一个重要的假设：一阶马尔可夫性——k时刻状态只与k-1时刻状态有关，整理成两个要素如下：

• $x_{k-1}$ contains the whole history
• $x_k = f(x_{k-1}, u_k, z_k)$

在这里我们只需要维护一个状态量$x_k$，并对它不断进行迭代更新，moreover，如果状态量服从高斯分布，我们只需要维护状态量的均值和方差即可（进一步简化）。

首先考虑一个线性系统：

卡尔曼滤波器的第一步预测，通过运动方程确定$x_k$的先验分布，注意用不同的上标区分不同的概率分布：尖帽子$\hat x_k$表示后验，平帽子$\bar x_k$表示先验：

第二步为观测，通过分析实际观测值，计算在某状态下应该产生怎样的分布：

第三步为更新，根据第一节中的贝叶斯法则，得到$x_k$的后验分布：

整体的流程图如下：

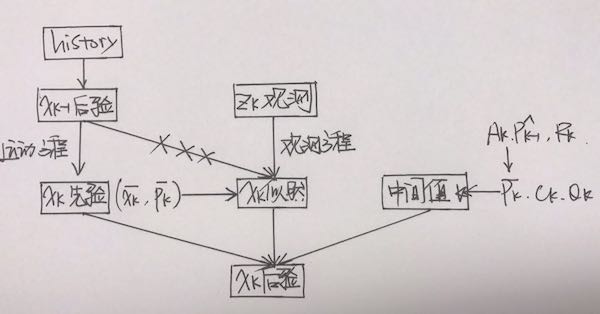
具体过程本节中不做展开，详情可以参考卡尔曼滤波。高斯分布经过线性变换仍然服从高斯分布，因此整个过程没有发生任何的近似，因此可以说卡尔曼滤波器构成了线性系统的最优无偏估计。

下面考虑非线性系统：

SLAM中不管是三维还是平面刚体运动，因为都引入了旋转，因此其运动方程和观测方程都是非线性函数。一个高斯分布，经过非线性变换，通常就不再服从高斯分布，因此对于非线性系统，必须采取一定的近似，将一个非高斯分布近似成高斯分布。

通常的做法是，将k时刻的运动方程和观测方程在$\hat x_{k-1}$，$\hat P_{k-1}$处做一阶泰勒展开，得到两个雅可比矩阵：

中间量卡尔曼增益$K_k$：

后验概率：

对于SLAM这种非线性的情况，EKF给出的是单次线性近似下的最大后验估计（MAP）。

4. EKF VS Graph-Optimization

1. 马尔可夫性抛弃了更久之前的状态，优化方法则运用了更多的信息。
2. 非线性误差：两种方法都使用了线性化近似，EKF只在$x_{k-1}$处做了一次线性化，图优化法则在每一次迭代更新时都对新的状态点做泰勒展开，其线性化的模型更接近原始非线性模型。
3. 存储：EKF维护的是状态的均值和方差，存储量与状态维度成平方增长，图优化存储的是每个状态点的位姿，存储线性增长。

Ceres

使用Ceres求解非线性优化问题，主要分为三个部分：

• 第一部分：构建代价函数Cost_Functor

  1 2 3 4 5 6 7 8

  // 定义一个实例化时才知道的类型T template <typename T> // 运算符()的重载，用来得到残差fi bool operator()(const T* const x, T* residual) const { residual[0] = T(10.0) - x[0]; return true; }

• 第二部分：构建最小二乘问题problem

  1 2 3 4 5

  Problem problem; // 使用自动求导，第一个1是输出维度（残差项），第二个1是输入维度（优化项） CostFunction* cost_function = new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor); // 添加误差项，NULL表示不使用核函数，x是优化项 problem.AddResidualBlock(cost_function, NULL, &x);

• 第三部分：求解器参数配置Solver

  1 2 3 4 5 6 7

  Solver::Options options; options.linear_solver_type = ceres::DENSE_QR; //配置增量方程的解法，稠密的QR分解 options.minimizer_progress_to_stdout = true;//输出到cout Solver::Summary summary;//优化信息 Solve(options, &problem, &summary);//求解 cout << summary.BriefReport() << "\n";//输出优化的简要信息

使用核函数：数据中往往存在离群点，离群点会对寻优结果造成影响，这时可以使用一些损失核函数来对离群点的影响加以消除，Ceres库中提供的核函数主要有：TrivialLoss 、HuberLoss、 SoftLOneLoss 、 CauchyLoss。

1
2

// 使用核函数
problem.AddResidualBlock(cost_function, new CauchyLoss(0.5, &x);

g2o

用g2o优化库来进行优化的步骤如下：

1. 定义节点和边的类型，通常在默认的基础类型上做修改

   定义顶点，顶点的基类为g2o::BaseVertex<优化变量维度，数据类型>

   1	class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>

   顶点的更新函数oplusImpl：定义增量加法，因为优化变量和增量之间并不一定是线性叠加的关系，如位姿变换。

   定义边， 本例中的边为一元边，基类为g2o::BaseUnaryEdge<观测值维度，数据类型，连接顶点类型>

   1	class CurveFittingEdge: public g2o::BaseUnaryEdge<1, double , CurveFittingVertex>

   误差项计算函数computeError：计算预测值和观测值的误差。估计值是基于当前对优化变量的estimate计算出的，观测值是直接获取的，如本例中的y值。

1. 构建图模型

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

   // vertex g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); // camera pose pose->setId( index ); pose->setEstimate( expression ); optimizer.addVertex ( pose ); // edge g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV(); edge->setId ( index ); edge->setVertex ( 0, point ); edge->setVertex ( 1, pose ); edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) ); // 导入观测值 edge->setParameterId ( 0,0 ); edge->setInformation ( Eigen::Matrix2d::Identity() ); // 设置信息矩阵 optimizer.addEdge ( edge );

   信息矩阵edge->setInformation(信息矩阵)：因为最终的优化函数是$\sum e_i^T \Sigma^{-1}e_i$，是误差项和信息矩阵乘积的形式。

2. 优化器配置

   • 矩阵块Block
   • 优化算法solver
   • 图模型optimizer

3. 执行优化

前面说完了 PnP，趁热打铁更新直接法，因为两者的思路基本一致，主要的差别在于PnP中利用的是特征点的重投影误差——匹配点在query帧像素平面上的实际位置和估计位置的误差，直接法不提取特征点，而是采用像素亮度误差。

1. 直接法的推导

以第一个相机为参考系，第二个相机的运动参数为$R, t, \xi$，对某个空间点$P$：

两个像素点的亮度误差：

目标函数：

误差函数关于优化变量的导数：

上面的扰动相关项中，记：

误差函数线性化：

$q$表示扰动分量在第二相机坐标系下的坐标（回顾关于$R$的微分方程：$\dot R(t) = \phi_0^{\wedge}R(t)$），因此$u$的意义为像素坐标，$\frac{\partial I_2}{\partial u}$的物理意义为像素梯度，$\frac{\partial u}{\partial q}$的物理意义为像素坐标关于三维点的导数（参考针孔相机模型），$\frac{\partial q}{\partial \delta \xi}$的物理意义为三维点关于扰动的导数（参考李代数）。

2. 直接法分类

根据P的来源，直接法分为三类：

1. P来自于稀疏关键点——稀疏直接法
2. P来自部分像素，只使用带有梯度的像素点——半稠密直接法
3. P为所有像素——稠密直接法

3. 代码实现

主要关注Edge类里面重定义的增量更新函数linearizeOplus()里面Jacobian矩阵的写法。

• 前一项是$u$处的像素梯度，使用数值导数：

1
2
3
4

// jacobian from I to u (1*2)
Eigen::Matrix<double, 1, 2> jacobian_pixel_uv;
jacobian_pixel_uv ( 0,0 ) = ( getPixelValue ( u+1,v )-getPixelValue ( u-1,v ) ) /2;
jacobian_pixel_uv ( 0,1 ) = ( getPixelValue ( u,v+1 )-getPixelValue ( u,v-1 ) ) /2;

• getPixelValue这个函数涉及到一个双线性插值，因为上面的二维坐标uv是通过相机投影变换得到的，是浮点形式，而像素值是离散的整数值，为了更精细地表示像素亮度，要对图像进行进行插值。

  • 线性插值：已知数据$(x_0, y_0)$和$(x_1, y_1)$，要计算$[x_0, x_1]$区间内任一$x$对应的$y$值：
  $$\frac{y - y_0}{x-x_0} = \frac{y_1-y_0}{x_1-x_0}\\ \therefore y = \frac{x_1 -x}{x_1 - x_0}y_0 + \frac{x-x_0}{x_1-x_0}y_1$$

  • 双线性插值：本质上就是在两个方向上做线性插值：

    

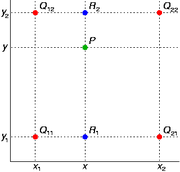
    首先是x方向：

    $$f(R_1) = \frac{x_2 - x}{x_2-x_1}f(Q_{11}) + \frac{x - x_1}{x_2-x_1}f(Q_{21}), \ where\ R_1 = (x, y_1)\\ f(R_2) = \frac{x_2 - x}{x_2-x_1}f(Q_{12}) + \frac{x - x_1}{x_2-x_1}f(Q_{22}), \ where\ R_2 = (x, y_2)$$

    然后y方向：

    $$f(P) = \frac{y_2 - y}{y_2 - y_1}f(R_1) + \frac{y-y_1}{y_2-y_1}f(R_2)$$

    综合起来就是：

    $$f(x,y) = \frac{f(Q_{11})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y_2-y) + \frac{f(Q_{21})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y_2-y) \\ + \frac{f(Q_{12})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y-y_1) + \frac{f(Q_{22})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y-y_1)$$

1
2
3
4
5
6
7
8
9
10
11

inline float getPixelValue ( float x, float y )
{
    uchar* data = & image_->data[ int ( y ) * image_->step + int ( x ) ];
    float xx = x - floor ( x );
    float yy = y - floor ( y );
    return float (
            ( 1-xx ) * ( 1-yy ) * data[0] +
            xx* ( 1-yy ) * data[1] +
            ( 1-xx ) *yy*data[ image_->step ] +
            xx*yy*data[image_->step+1]
    );

• 后两项都是与相机参数和三维点坐标有关，可以合并，同时注意g2o中对SE3的定义平移和旋转和本文设定是反过来的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

// jacobian from u to xi (2*6)
Eigen::Matrix<double, 2, 6> jacobian_uv_ksai;
// xi = [\phi, \pho]
jacobian_uv_ksai ( 0,0 ) = - x*y*invz_2 *fx_;
jacobian_uv_ksai ( 0,1 ) = ( 1+ ( x*x*invz_2 ) ) *fx_;
jacobian_uv_ksai ( 0,2 ) = - y*invz *fx_;
jacobian_uv_ksai ( 0,3 ) = invz *fx_;
jacobian_uv_ksai ( 0,4 ) = 0;
jacobian_uv_ksai ( 0,5 ) = -x*invz_2 *fx_;

jacobian_uv_ksai ( 1,0 ) = - ( 1+y*y*invz_2 ) *fy_;
jacobian_uv_ksai ( 1,1 ) = x*y*invz_2 *fy_;
jacobian_uv_ksai ( 1,2 ) = x*invz *fy_;
jacobian_uv_ksai ( 1,3 ) = 0;
jacobian_uv_ksai ( 1,4 ) = invz *fy_;
jacobian_uv_ksai ( 1,5 ) = -y*invz_2 *fy_;

1. cmake选项

• 测试单元可以关掉：BUILD_DOCS，BUILD_EXAMPLES，BUILD_XXX_TESTS，BUILD_opencv_ts(一些单元测试代码)，BUILD_PACKAGE (CPACK_BINARY_XXX，CPACK_SOURCE_XXX)，INSTALL_XXX
• 减少引入体积：打开世界模块开关BUILD_opencv_world(暂时没开，因为编译之后发现找不到要引用的头文件了)，打开BUILD_SHARED_LIBS
• 关掉音视频处理相关模块：BUILD_opencv_video，BUILD_opencv_videoio，BUILD_opencv_videostab，WITH_1394，WITH_GSTREAMER_XXX
• 关闭GPU相关模块：WITH_OPENCL，WITH_CUDA
• 打开TBB模块：隐式的并行计算程序，底层依赖于操作系统的多线程库，BUILD_TBB
• 打开viz模块：WITH_VTK，BUILD_opencv_viz
• 暂时没开启Java相关模块：ant，就没brew过这个包

以上reference from 博客1，博客2

2. extra modules

with opencv3.0, SURF/SIFT and some other things have been moved to a seperate opencv_contrib repo.

一部分模块被独立到了opencv_contrib这个包，首先clone到本地，然后在cmake选项里面找到OPENCV_EXTRA_MODULES_PATH，填好。

2. 其他说明

另外之前brew install的opencv包一定要卸载掉，不要乱link，否则INCLUDE和LIBS的路径都会出问题，手动修改cmake文件不要太酸爽。

1. 概述

PnP是求解3D到2D点对运动的方法，它描述了当知道n个3D空间点及其投影位置时，如何估计相机的位姿变换。最少只需要3个点对就可以估计相机的运动。

该方法使用的条件是，参考点为世界坐标系下的特征点，其空间位置已知，并且知道query帧中对应参考点的像素坐标。

PnP问题的求解方法有很多种：

• 直接线性变换
• P3P
• 非线性优化方法——Bundle Ajustment

本节着眼于BA求解方法，其他方法暂时不做展开。

2. Bundle Ajustment

利用优化求解的思路是：最小化重投影误差——期望计算query帧的相机位姿$R, t$，它的李代数为$\xi$，空间特征点的坐标为$P_i = [X_i, Y_i, Z_i]^T$，其在query帧上的像素坐标为$u_i = [u_i, v_i]^T$，那么理论上：

构建成最小二乘问题就是：寻找最优的相机位姿$\xi$，使得误差最小化：

在使用优化库来求解之前，还有一个问题——每个误差项$e_i = u_i -\frac{1}{s_i}Kexp(\xi^{\wedge})P_i$的导数$J_i$。

回忆图优化中讲过的，优化问题最终转化成为矩阵的线性求解$H\Delta x = g$，其中矩阵$H$是由单个误差项一阶展开$e(x+\Delta x) = e(x) + J\Delta x$中的雅可比矩阵$J_i$ 构成的稀疏对称阵。

误差项是一个二维向量（像素坐标差），优化变量是一个六维向量（空间位姿李代数），因此$J$是一个2*6的矩阵。

其中$P^{‘}$是特征点转换到相机坐标系下的空间坐标：

因此误差项导数的第一项为：

误差项的第二项为变换后的点关于李代数的导数，参考李代数节：

其中$P^{‘\wedge}$是$P^{‘}$的反对称阵：

因此得到完整的雅可比矩阵：

除了优化相机位姿以外，还可以同时优化特征点的空间位置$P$：

其中的第二项为：

3. 优化库使用

构建图模型：

• 优化变量1：节点1：query相机位姿（六维向量李代数）
• 优化变量2：节点2：特征点空间位置（三维向量坐标描述）
• 预测值：边n：根据当前estimate的优化量，投影到投影平面的像素坐标$z_i = h(\xi, P_i)$
• 观测值：能够直接读出的，query帧上对应特征点的实际投影坐标$u_i$

g2o中已经提供了相近的基类（在g2o/types/sba/types_six_dof_expmap.h中）：李代数位姿节点VertexSE3Expmap、空间点位置节点VertexSBAPointXYZ、投影方程边EdgeProjectXYZ2UV。

边类里面要关注linearizeOplus函数，这个函数描述的是非线性函数进行线性化的过程中，求导的解析解（当然也可以使用数值解），最后函数给出的是每个节点的导数矩阵（$\frac{\partial e}{\partial \delta \xi} $和$\frac{\partial e}{\partial P_i}$） 。这点是Ceres库和g2o库的一点主要差别：Ceres都是使用自动的数值导数，g2o要自己求导。

1
2
3
4
5
6
7
8
9
10
11

void EdgeProjectXYZ2UV::linearizeOplus()
{
    VertexSE3Expmap * vj = static_cast<VertexSE3Expmap*>(_vertices[1]);
    VertexSBAPointXYZ* vi = static_cast<VertexSBAPointXYZ*>(_vertices[0]);
    ...
    ...
    _jacobianOplusXi = -1./z * tmp * T.rotation().toRotationMatrix();
 
    _jacobianOplusXj(0,0) = x*y/z^2 * cam->focal_length;
    ...
}

4. OpenCV内置函数

basic：

1
2
3
4
5

void cv::solvePnP ( pts3d, pts2d, K, Mat(), r, t, false );

Mat r, t, R;
cv::solvePnP ( pts3d, pts2d, K, Mat(), r, t, false );
cv::Rodrigues ( r, R );     // 旋转向量和旋转矩阵的转换

advanced：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

bool cv::solvePnPRansac( 
    InputArray objectPoints,      // 3D空间坐标 vector<cv::Point3f> pts3d
    InputArray imagePoints,       // 2D像素坐标 vector<cv::Point2f> pts2d
    InputArray cameraMatrix,      // 相机内部参数矩阵 K
    InputArray distCoeffs,        // 畸变系数向量 cv::Mat()
    OutputArray rvec,             // 旋转向量
    OutputArray tvec,             // 平移向量
    bool useExtrinsicGuess = false, // If true, the function uses the provided rvec and tvec values as initial
    int iterationsCount = 100,    // Number of iterations
    float reprojectionError = 8.0,// 重投影误差最大值
    double confidence = 0.99,
    OutputArray inliers = noArray(), // Output vector that contains indices of inliers in objectPoints and imagePoints .
    int flags = SOLVEPNP_ITERATIVE   // method for solving PnP
)

• Ransac：考虑到我们提供的匹配里面存在误匹配的情况，OpenCV采用“随机采样一致性算法”（Random Sample Consensus），从现有匹配中随机取一部分用来估计运动（PnP的解析解法最少只需要三个点就能计算相对位姿），正确的匹配结果都是近似的，从而剔除误匹配。
• inlier：内点，函数最终给出的匹配可信的点。
• RANSAC只采用少数几个随机点来计算PnP，容易受到噪声影响。工程上通常使用RANSAC的解作为初值，再使用非线性优化方法求解最优值。

1
2
3
4
5
6
7
8
9
10
11
12
13

// Ransac粗匹配
cv::solvePnPRansac( pts3d, pts2d, K, Mat(), rvec, tvec, false, 100, 4.0, 0.99, inliers );
cv::Rodrigues ( rvec, R ); 
Eigen::Matrix3d rotation_matrix = R.at<double>;
T_c_r_estimated_ = SE3d(
        SO3d(rotation_matrix),
        Vector3d( tvec.at<double>(0,0), tvec.at<double>(1,0), tvec.at<double>(2,0))
    );
    
// BA局部优化
g2o::VertexSE3Expmap* pose new g2o::VertexSE3Expmap();
...
pose->setEstimate(g2o::SE3Quat( T_c_r_estimated_.rotationMatrix(), T_c_r_estimated_.translation()));

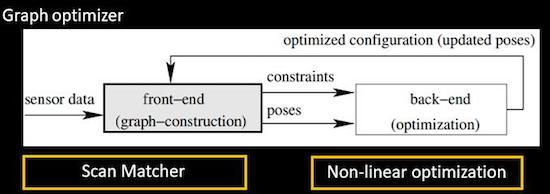
基于极其标准的图优化SLAM框架来实现：

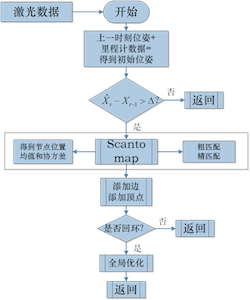
提出了采用稀疏点调整（SPA）的方法来高效求解位姿图优化问题，针对本算法的文献为《Efficient Sparse Pose Adjustment for 2D Mapping》。

scan matching部分的参考文献为《Real-time correlative scan matching》，M3RSM的前身！

key concepts：

• keyScan：机器人运动一定的距离或角度（关键帧），储存在sensorManager，无地图缓存。

• look-up table查找表：查找表的意义就是相比于暴力匹配，不需要每次都重新计算每个激光数据信息，相同角度不同位置的激光数据信息只需要被索引一次。

• response响应值：将查找表以一定的位移投到子图上，总共有n个点被查找表击中（hit），击中的每个点得分不同（score），累加得分并除以可以达到的最高分。

  $$response = \frac{\sum_{i=0}^n goal_i}{goalmax}$$

• 协方差：文献专门用了一节计算协方差，但是没看到用在哪，是为了后面求误差做准备吗？？？

• addScans添加顶点和边：边是误差值，添加的边约束来自两部分，

  （1）link to running scans，距当前帧一定范围内的激光数据链（RunningScan chain）。

  （2）link to other near chains，从当前节点开始广度优先遍历一定距离范围内所有节点，依据当前id从sensorManager中分别递增和递减寻找一定范围内的chain（不一定直接相连）。

• 回环检测：操作与添加边约束类似，位姿图上要去除那些和当前节点的时间相邻的节点。

  （1）找到一定距离范围内（near）和相连（adjacent）的节点添加进nearLinkedScans。

  （2）MapperGraph::FindPossibleLoopClosure：从sensorManager中从前到后，依据序号挑选与当前节点在一定距离范围内，且不在nearLinkedScans中的candidate。返回潜在chain。其中涉及两个参数：

  • LoopSearchMaximumDistance：candidateScan与当前scan的距离必须在可容许的距离内。
  • LoopMatchMinimumChainSize：chain中的节点数必须不小于限定值。

  （3）MapperGraph::TryCloseLoop：scan2map匹配，当response和covariance达到一定要求认为闭环检测到，得到correct pose（也就是认为candidateScan的pose才是当前帧的实际pose）。

  （4）add link to loop，构成全局闭环。

  （5）触发correctPose，进行spa优化。

代码随手记：

1. ROS上面提供三个开源包：nav2d_karto, open_karto, slam_karto。

   ROS Wiki上这么描述nav2d_karto这个package：Graph-based Simultaneous Localization and Mapping module. Includes OpenKarto GraphSLAM library by “SRI International”.

   open_karto：开源的karto包，实现底层的kartoslam

   slam_karto：ros层，应用层的kartoslam接口

2. The LaserRangeFinder contains parameters for physical laser sensor used by the mapper for scan matching Also contains information about the maximum range of the sensor and provides a threshold for limiting the range of readings.

   The optimal value for the range threshold depends on the angular resolution of the scan and the desired map resolution.

3. resolution：0.25 & 0.5 & 1 degree

   number of range readings (beams)：（maximumAngle - minimumAngle）／angularResolution + 1

4. GridStates：0 for Unknown，100 for Occupied， 255 for Free。

5. flipY：最开始机器人应该处在世界坐标系的原点，传感器坐标系与机器人baselink存在一个坐标变换，原始的传感器坐标系位置应该与地图坐标系重合，这就是world和grid之间的offset。flip是啥呢？？

6. LookupArray[index]：Create lookup tables for point readings at varying angles in grid. This is to speed up finding best angle/position for a localized range scan

7. MapperGraph：花式构造位姿图

8. CorrelationGrid：Implementation of a correlation grid used for scan matching

9. Region of Interest ROI：

10. smear：The point readings are smeared by this value in X and Y to create a smoother response. 个人理解这句话是说点容易生成突变，用以点为中心的一小片区域平滑一点。

11. ScanMatch：返回响应值response

    前端匹配调用m_pSequentialScanMatcher->MatchScan

    闭环检测调用m_pLoopScanMatcher->MatchScan

    两个函数继承于ScanMatcher::MatchScan：

    1 2 3 4 5 6 7 8

    kt_double ScanMatcher::MatchScan( LocalizedRangeScan* pScan, const LocalizedRangeScanVector& rBaseScans, Pose2& rMean, Matrix3& rCovariance, kt_bool doPenalize, kt_bool doRefineMatch) // default is True, 决定是否做精匹配 // @return: strength of response (best response)

    其中会调用ScanMatcher::CorrelateScan方法。ScanMatcher::CorrelateScan方法中调用ScanMatcher::GetResponse方法计算响应值。

    1 2 3

    kt_double ScanMatcher::GetResponse( kt_int32u angleIndex, kt_int32s gridPositionIndex) const

    GetResponse的核心在kt_int8u* pByte和const LookupArray* pOffsets两个数据结构：

    • 前者是在correlationGrid范围内的real sensed占据情况。

    • 后者是lookup-table中（已知地图）读取的栅格占据情况，只包含占据的栅格，key是angular。

      计算response只要看地图上的占据点是否在观测中是否也是占据的：

      1 2 3 4 5 6 7 8 9 10 11 12

      for (kt_int32u i = 0; i < pOffsets->GetSize(); i++) { // ignore points that fall off the grid kt_int32s pointGridIndex = gridPositionIndex + pAngleIndexPointer[i]; if (!math::IsUpTo(pointGridIndex, m_pCorrelationGrid->GetDataSize()) || pAngleIndexPointer[i] == INVALID_SCAN) { continue; } // uses index offsets to efficiently find location of point in the grid response += pByte[pAngleIndexPointer[i]]; }

      最终的response要normalize：

      1 2 3

      // normalize response response /= (nPoints * GridStates_Occupied); // GridStates_Occupied = 100, assert(fabs(response) <= 1.0);

12. karto只在闭环的时候触发后端优化CorrectPoses()，ScanSolver的实现在Samples路径下的SpaSolver，调用了现有的BA求解器sba(A Generic Sparse Bundle Adjustment C/C++ Package Based on the Levenberg-Marquardt Algorithm)。

参数&优化方向

1. 闭环中candidate数量的调整：
   • 减小LoopSearchMaximumDistance，进入candidate范围的节点数据减少
   • 减小LoopMatchMinimumChainSize，用来计算优化的candidate数量减少
   • 增大minimum_travel_distance和minimum_travel_heading，这样总体的节点数减少
2. Map_update_interval：发布地图的间隔，其主要过程是遍历当前所有节点数据，对每个栅格的占有状态进行判定，生成栅格地图。
3. ScanBufferSize和ScanBufferMaximumScanDistance：控制buffer也就是chain的大小。chain不能太大也不能太小，太小会造成前端误差累积，太大会导致构建闭环的节点数不足。推荐值是ScanBufferMaximumScanDistance／minimum_travel_distance。
4. 位姿纠正中：
   • CorrelationSearchSpaceDimension：The size of the search grid
   • CorrelationSearchSpaceResolution：The size of the correlation grid
5. 回环检测中：
   • LoopSearchMaximumDistance：闭环检测的搜索距离，数值越大能越早发现闭环，也能容忍更大的偏离误差。
   • LoopMatchMinimumResponseCoarse和LoopMatchMinimumResponseFine：粗匹配和精匹配的响应阈值，与闭环中candidate数量相关。阈值过低会导致candidate迅速被填满，真正好的点还没找到。阈值过高会导致回环失败（一直找不到回环点），地图上出现重影。

CPU Usage

算法资源占用的主要压力来源：

1. 地图更新
2. 回环检测
3. SPA优化

lc79

挂一道很猥琐的题，二维网格中搜索单词，同一单元格不能重复使用：

1
2
3
4
5
6
7
8
9
10

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

给定 word = "ABCCED", 返回 true.
给定 word = "SEE", 返回 true.
给定 word = "ABCB", 返回 false.

没啥好算法，就是DFS，但是坑在于visited的存储，python数组默认浅拷贝，递归传进去再回到上一层网格状态就变了，之前一贯的做法就是新开一块内存空间，传新的数组进去，然而这次超时了，因为测试用例的二维数组尺寸贼大，终于有机会正视这个问题，并获取正确的打开方式：

• 尺寸贼大的二维数组，每次只需要修改一个值，重新划空间拷贝再修改时间复杂度瞬间增大O(m*n)倍，很明显传原来的数组进去比较合适。

• 但是深层递归会修改传进去的参数，因此在每次递归之前先创建一个tmp，记录修改行为，递归函数进行完以后，再根据记录恢复原来的参数，保证本层参数不变。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  def search_tail(board, word, h, w): size = len(word) char = word[0] height, width = len(board), len(board[0]) exist = False if h - 1 >= 0 and board[h-1][w] == char: if size == 1: return True else: tmp = board[h-1][w] board[h-1][w] = 'INF' exist = search_tail(board, word[1:], h-1, w) if exist: return True board[h-1][w] = tmp if h + 1 < height and board[h+1][w] == char: ... ...

• 然后针对本题还有一个骚操作，很多人专门创建一个visited表来记录搜索路径，但是因为本题的二维数组限定存储字母，所以任意一个非字母都可以作为标志位，美滋滋又省下一个O(m*n)。

lc81

实名diss这道题，一看是旋转排序数组直接做了，然后才发现测试样例里面出现了左右边界重合的情况，然后仔细再审题才发现这行小字：

这是搜索旋转排序数组的延伸题目，本题中nums可能包含重复元素

不包含重复元素的情况下代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution:
    def search(self, nums, target):

        size = len(nums)
        start = 0
        end = size - 1
        while start <= end:

            mid = (start + end) // 2
            if nums[mid] == target:
                return True

            if nums[mid] <= nums[end]:
                if target < nums[mid] or target > nums[end]:
                    end = mid - 1
                else:
                    start = mid + 1

            else:
                if target > nums[mid] or target < nums[start]:
                    start = mid + 1
                else:
                    end = mid - 1

        return False

因为数组中现在存在重复的元素，因此有一个特殊的情况：左右边界值相同，并且nums[mid]值与边界值也相同，这时nums[mid]可能位于两段数组的任意一边。因此要独立讨论一下这个情况：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution:
    def search(self, nums, target):

        size = len(nums)
        start = 0
        end = size - 1
        while start <= end:

            mid = (start + end) // 2
            if nums[mid] == target:
            	return True

            if nums[mid] < nums[end]:
            if target < nums[mid] or target > nums[end]:
                end = mid - 1
            else:
                start = mid + 1

            elif nums[mid] > nums[end]:
                if target > nums[mid] or target < nums[start]:
                    start = mid + 1
                else:
                    end = mid - 1

            # nums[mid] = nums[end]的情况
            else:
            	end -= 1
		
        return False

测试用时50ms，因为边界重复的循环没有有效地二分数组，但是思路贼简单啊。

lc95

96和95都是二叉搜索树，先做的96，求树的结构有几种，没注意结点大小关系，用动态规划来做，$dp[i] = dp[0]dp[i-1] + … + dp[i-1]dp[0]$。注意递归调用的时间复杂度，自底向上来算：

1
2
3
4
5
6
7
8
9
10
11

def numTrees(self, n):
	res = [1, 1]
    if n < 2:
        return res[n]
    
    res += [0]*(n-1)
    for i in range(2, n+1):
        for j in range(i):
            res[i] += res[j]*res[i-1-j]
	
    return res[n]

95要列出结构了，才发现什么是二叉搜索树来着——左子树的结点值均小于根节点，右子树的结点值均大于根节点。按照惯例，求数量用DP，求枚举则用DFS：

遍历每一个数字$i$作为根节点，那么$[1, 2, …, i-1]$构成其左子树，$[i+1, i+2, …, n]$构成其右子树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

def generateTrees(self, n):
	if n == 0:
        return []
    return self.dfs(1,n)


def dfs(self, b, e):
    if b > e:
        return [None]
    res = []
    for i in range(b, e+1):
        # set as the root node
        leftTrees = self.dfs(b, i-1)
        rightTrees = self.dfs(i+1, e)
        for left in leftTrees:
            for right in rightTrees:
                root = TreeNode(i)
                root.left = left
                root.right = right
                res.append(root)
	return res

lc28

实现 strStr() 函数。给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

KMP算法，两个难点：

• O(m)计算needle中每个子串 needle[:k]的最长前缀
• O(n)计算无回溯匹配needle

【先分析第一个：

needle的长度为m，那么维护一个等长的前缀数组next，next[0]=0，首字母没有真正意义的前/后缀

对于子串needle[:i]，首先查看子串needle[:i-1]的前缀长度，j=next[i-1]

• 如果needle[j]=needle[i]，next[i]=j+1
• 如果不相等，我们目前有needle[:i-1]的前/后缀，needle[0:j]和needle[i-j:i]，显然needle[:i]的前缀只能是needle[0:j]的前缀子串，最长为needle[0:j-1]，同时它还得是needle[i-j:i]的后缀子串，说白了就是在子串needle[0:j]中要最大匹配前/后缀：迭代j=next[next[i-1]-1]，如果子串没有共享前/后缀就是0

1
2
3
4
5
6
7
8
9
10

next = [0] * len(needle)
for i in range(1,len(needle)):
	j = next[i-1]
	while j>0 and needle[i]!=needle[j]:
		j = next[j-1]
        
	if needle[i]==needle[j]:
		next[i] = j+1

print('next', next)

【再分析查找阶段，对于给定字符串haystack，暴力解法是从头开始匹配，遇到mismatch就回溯到起始点下一位重新开始匹配，这样的时间复杂度是O(nm)，之所以能够做到无回溯匹配，就是因为有了前缀数组，当我们匹配到needle的一半遇到mismatch了，对于已经匹配上的子串，不需要回溯到起始位置，而是可以从共享前/后缀开始匹配，

1
2
3
4
5
6
7
8
9

needle_idx = 0
for i in range(len(haystack)):
	while needle_idx and haystack[i]!=needle[needle_idx]:
		needle_idx = next[max(0,needle_idx-1)]
	if haystack[i]==needle[needle_idx]:
		needle_idx += 1
	if needle_idx>=len(needle):
		return i-len(needle)+1
return -1

lc215

求无序数组中第k个最大元素，题目里的O(n)比较有迷惑性，本来想保留一个含k个大元素的动态数组，一次遍历，但每次插值要O(klogk)，总体的复杂度是O(nklogk)，整个数组排序的复杂度是O(nlogn)，所以直接排序：

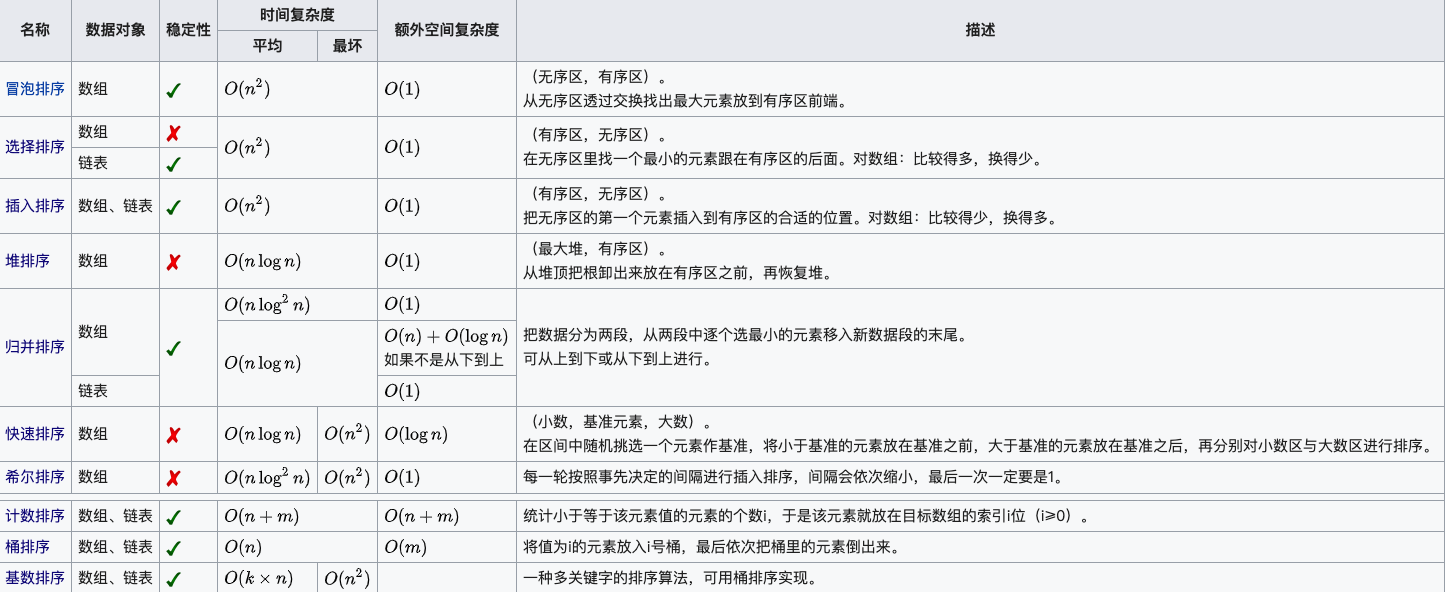
1. 快排

   算法：随机挑选一个基点pivot，把所有小于它的数都放在它左边，所有大于它的数都放在它右边，对左右两个partition递归进行上述操作，算法复杂度是O(nlogn)

   稳定性：不是稳定排序，每次放置的位置并不是严格有序的

   优化：partition的过程是原地的，求第K个数的时候可以early stop，不需要严格排序所有segment

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

   def findKthLargest(self, nums: List[int], k: int) -> int: def sort_partition(left, right): if left>=right-1: return i, j = left, right-1 while i<j: # pivot at i: move right ptr while i<j and nums[i]<=nums[j]: j -= 1 nums[i], nums[j] = nums[j], nums[i] # pivot at j: move left ptr while i<j and nums[i]<=nums[j]: i += 1 nums[i], nums[j] = nums[j], nums[i] # early stop in this case if i==len(nums)-k: return nums[i] if i>len(nums)-k: sort_partition(left, i) else: sort_partition(i+1, right) # quick sort sort_partition(0, len(nums)) # return the k-th return nums[-k]

2. 堆排序

   堆是完全二叉树：除了最底层之外，每一层都是满的，因此可以推算给定节点的父结点和子结点

   • given node i：下标从0开始
   • parent id =(i-1)//2
   • children id = [2i+1, 2i+2]
   • 最大堆：每个parent node的值都大于其children node

   • 最小堆：每个parent node的值都小于其children node

     算法：依次提取堆顶元素，然后重组剩余节点

     稳定性：不稳定

   • 给定一个无序数组，如何建立为堆？从队尾开始遍历每个非叶子节点，递归调整树结构

     1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

     def maxHeapify(lst, i, heap_size): left, right = i*2+1, i*2+2 largest = i if left<heap_size and lst[left]>lst[largest]: largest = left if right<heap_size and lst[right]>lst[largest]: largest = right if largest!=i: # swap lst[i], lst[largest] = lst[largest], lst[i] maxHeapify(lst, largest, heap_size) def build(lst): # build heap from the last parent node n = len(lst) for i in range(n//2, -1, -1): maxHeapify(lst, i, n)

   • 删除堆顶元素后，如何调整数组成为新堆？用堆尾元素替换堆顶元素，然后逐渐下沉

     1 2 3 4 5 6 7

     def heap_sort(lst): # take top & ajust the rest current_idx = n-1 while current_idx>0: lst[0], lst[current_idx] = lst[current_idx], lst[0] maxHeapify(lst, 0, current_idx) current_idx -= 1

3. 归并排序

   算法：依次合并有序的子序列得到有序数组，有递归和迭代两种实现方式，需要额外的空间来合并子序列，不是原地排序，算法复杂度为O(nlogn)，空间复杂度为O(n)+O(logn)

   稳定性：子序列永远升序，是稳定排序

4. 冒泡排序

   算法：依次比较相邻元素，如果左>右，就交换，每轮参与比较的最大值会放在最尾部

   稳定性：在相邻元素相等时，它们不会交换位置，所以，冒泡排序是稳定排序

   优化：early stop，当检测到本轮比较已经没有需要swap的元素时，排序可以提前停止，此时升序数组复杂度为O(n)，倒序数组为O(n^2)

5. 插入排序

   算法：维护一个sorted lst和一个unsorted lst，每次从unsorted lst中拿一个元素插入进sorted lst相应位置

   稳定性：插入新元素不会打乱已有排序，是稳定排序

   优化：查找insert idx时候可以用二分查找减少查找次数，查找次数在logn～n之间，总体的时间复杂度还是O(n^2)

Reference：Bentley J L. Multidimensional Binary Search Trees Used for Associative Searching[J]. Communications of the Acm, 1975, 18(9):509-517.

前面更新basic ICP的时候留了一个坑——最近邻的求法。线性扫描？手动挥手。

1. 先说说距离吧

1.1 欧式距离

1.2 标准化欧式距离

首先将数据各维度分量都标准化到均值为0，方差为1，再求欧式距离：

简单推导后可以发现，标准化欧式距离实际上就是一种加权欧式距离：

1.3 马氏距离（Mahalanobis Distance）

其中$S$为协方差矩阵$Cov$：

若协方差矩阵是单位阵（样本各维度之间独立同分布），那公式就变成欧式距离了，若协方差矩阵是对角阵，那公式就变成标准化欧式距离了。

1.4 相似度

相似度也是距离的一种表征方式，距离越相近，相似度越高。

• 欧式距离相似度：将欧式距离限定在0 1之间变化

• 余弦相似度：-1到1之间变化

• 皮尔逊相关系数：-1到1之间变化

1

return numpy.corrcoef(A, B)

2. KD树

• k-NN算法
• 推荐系统
• SIFT特征匹配
• ICP迭代最近点
• 最近在做的M3RCM中的堆结构（这个有点牵强，因为不是二叉树）

总之以上这些基于匹配／比较的目的而进行的数据库查找／图像检索，本质上都可以归结为通过距离函数在高维矢量之间的相似性检索问题。

一维向量有二分法查找，对应地高维空间有树形结构便于快速检索。利用树形结构可以省去对大部分数据点的搜索，从而减少检索的计算量。

KD树是一种二叉树，通过不断地用垂直于某坐标轴的超平面将k维空间切分构造而成。

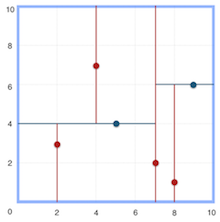
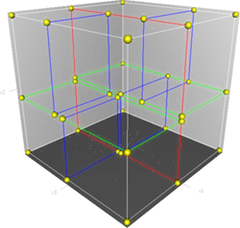
2.1 构造树

递归创建节点：节点信息包含切分坐标轴和切分点，从而确定超平面，将当前空间切分为左右两个子空间，递归直到当前子空间内没有实例为止。

1
2
3
4
5
6

class Node:
	def __init__(self, point, axis):
		self.value = point
		self.axis = axis
		self.left = None
		self.right = None

为了使得构造出的KD树尽可能平衡（高效分割空间）：

• 选择坐标轴：简单点的方式是循环交替选择坐标轴，复杂点的做法是选择当前方差最大的轴作为切分轴。
• 选择切分点：取选定坐标轴上数据的中值作为切分点。

注意：KD树的构造旨在高效分割空间，其叶子节点并非是最近邻搜索等应用场景的最优解。

1
2
3
4
5
6
7
8
9
10

def kdTree(points, depth):
	if len(points) == 0:
		return None
	axis = depth % len(points[0])
	points.sort(key=lambda x: x[axis])
	cut_idx = centreValue(points)
	node = Node(points[cut_idx], axis)
	node.left = kdTree(points[:cut_idx], depth+1)
	node.right = kdTree(points[cut_idx+1:], depth+1)
	return node

对于包含n个实例的k维数据来说，构造KD树的时间复杂度为O(k*n*log n)。

2.2 新增节点

递归实现：从根节点开始做比较，大于则插入左子树，小于则插入右子树。直到达到叶子节点，并创建新的叶子节点。

2.3 删除节点

将待删除的节点的所有子节点组成一个集合，重新构建KD子树，替换待删除节点。

2.4 最近邻搜索

搜索最近邻算法主要分为两部分：首先是深度优先遍历，直到遇到叶子节点，生成搜索路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

def searchNearest(node, target):
    # input: node: root node of the tree
    #        target: list
    # output: nearest: list
    # 	      dist: distance between target and nearest
    if node == None:
        return None
    # 生成搜索路径
    search_path = deque()
    nearest = node
    print("search path: ")
    while node:
        print(node.value)
        search_path.append(node)
        # if Dist(nearest.value, target) > Dist(node.value, target):
        # 	nearest.value = node.value
        # 	minDist = Dist(node.value, target)

        axis = node.axis
        if target[axis] > node.value[axis]:
            node = node.right
        else:
            node = node.left
    ...
    ...

然后是回溯查找，如果目标点和当前最近点构成的球形区域与其上溯节点相交，那么就有一种潜在的可能——上溯节点的另一个子空间的实例可能位于当前这个球形区域内，因此要进行一次判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

def searchNearest(node, target):
    # input: node: root node of the tree
    #        target: list
    # output: nearest: list
    # 	      dist: distance between target and nearest
    ...
    ...
    # 回溯
    print("\nsearch backwards: ")
    nearest = search_path.pop()
    minDist = Dist(nearest.value, target)

    while search_path:
        node = search_path.pop()
        print(node.value)
        if node.axis:
            axis = node.axis
            if minDist > Dist1(node.value[axis], target[axis]):
                if target[axis] > node.value[axis]:
                    search_path.append(node.left)
                else:
                    search_path.append(node.right)
        if Dist(target, nearest.value) > Dist(node.value, target):
            nearest = node
            minDist = Dist(node.value, target)
    return nearest.value, minDist

两个参考点：

1
2
3

samples = [(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)]
target = (2.1, 3.1)
target = (2, 4.5)

KD树搜索的核心就是：当查询点的邻域与分割超平面两侧空间交割时，需要查找另一侧子空间！！！算法平均复杂度O(N logN)。实际时间复杂度与实例分布情况有关，$t_{worst} = O(kN^{1-\frac{1}{k}})$，通常要求数据规模达到$N \geq 2^D$才能达到高效的搜索。

3. 改进算法：BBF算法

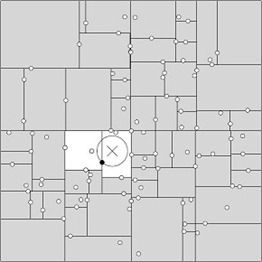
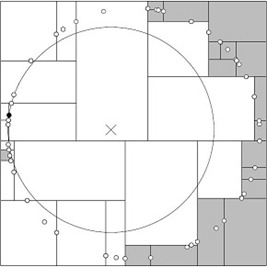
回溯是由查询路径决定的，因此一种算法改进思路就是将查询路径上的结点排序，回溯检查总是从优先级最高的树节点开始——Best-Bin-First BBF算法。该算法能确保优先检索包含最邻近点可能性较高的空间。

• 优先队列：优先级取决于它们离查询点的距离，距离越近，优先级越高，回溯的时候优先遍历。
• 对回溯可能需要路过的结点加入队列：切分的时候，把未选中的那个兄弟结点加入到队列中。