papers
[cvpr 2022] Deblurring via Stochastic Refinement
[SR3] SR3:Image Super-Resolution via Iterative Refinement
Deblurring via Stochastic Refinement
overview
- based on conditional diffusion models
- refines the output of a deterministic predictor
regress-based methods
- 通常用一个unet结构,直接回归clean image
- 训练数据是blur-clean pair
- ill posed:If there are multiple possible clean images that correspond to the blurry input, the optimal reconstruction according to the given loss function will be an average of them
- 通常结果比较平滑,细节纹理恢复不出来,我觉的是因为缺少noise sampling,只从确定的latent vec去做恢复
- unet regression将去噪task建模成了a to b的确定回归任务,但是实际上去噪的结果是多样的,更接近生成任务,从一个后验分布中生成并挑选不同的样本作为结果,说白了以前的方法是AE,现在的方法是VAE
DDPM
核心是两个公式
- 前向$q(x_t|x_0)$:given $x_0$,可以采样得到任意time step的$x_t$
- 后向$q(x_{t-1}|x_t,x_0)$:given $x_t$,可以随机denoise a single diffusion step得到$x_{t-1}$
优化目标
- 希望网络学到的$p_{\theta}(x_{t-1}|x_t)$接近真实的reverse diffusion step$q(x_{t-1}|x_t,x_0)$
- 方式就是最大化变分下界函数$log p_{\theta}(x)$
通过将x重参数化,将优化目标转换成noise的预测
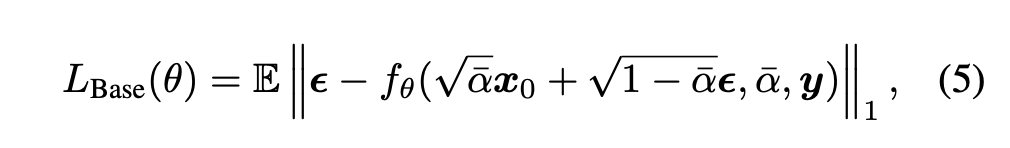
Continuous noise level
- allows us to sample from the model using a noise schedule α1:T different from the one used during training
- inference-time noise schedule和训练时不同,但是无需重新训练
Conditional DPM
- 我们的condition就是blur image
- 和输入concat在一起,x是3hw的noise/denoise input,y是3hw的blur prior
method
overview
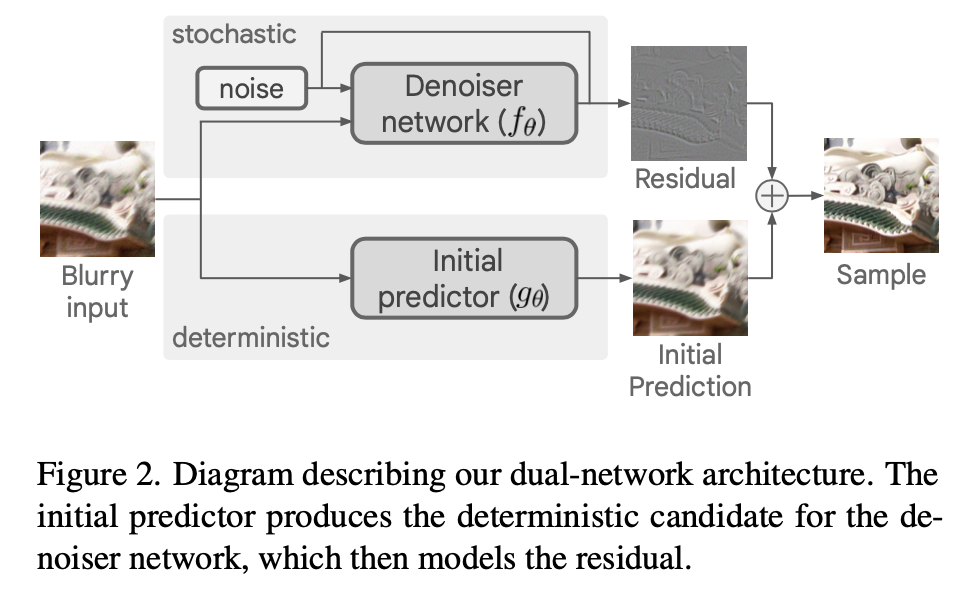
- 两部分网络
- initial predictor g:provides a data-adaptive candidate for the clean image
- denoiser network f:denoiser,only needs to model the residual
- 这样的好处是G可以做很大,F做很小
预测残差的话,x0-xT的定义也变为残差,优化目标里面的$x_0$改为$x_0-g_{\theta}(x_0)$
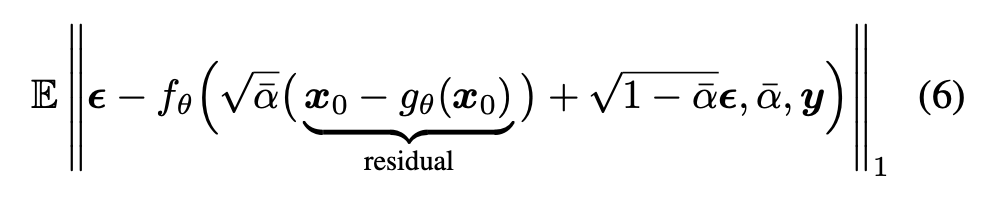
- 两部分网络
samping algorithm

- run G得到clean image的初始值$x_{init}$
- 随机采样正态分布得到初始input $z_T$
- from time step T到1:
- 随机采样一个
- reverse step:得到$z_{t-1}$
- 最后add初始值和residual得到最终预测
inference-time sampling
- 较高的step数和较低的噪声水平可以获得高感知的图像,better perceptual quality
- 较低的step数和较高的噪声水平可以获得高保真的图像,lower distortion
- 网格搜索noise schedule hyperparameters:就是DDIM的$\eta$和$\sigma$
- 两个超参:
- inference steps T from [10,20,30,50,100,200,300,500]
- noisy schedule $\alpha_T$
- 两个超参:
残差模型对图像进行采样所需的时间要少得多
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23# construct DDPM noise schedule
b_t = (beta2 - beta1) * torch.linspace(0, 1, timesteps + 1, device=device) + beta1
a_t = 1 - b_t
ab_t = torch.cumsum(a_t.log(), dim=0).exp()
ab_t[0] = 1
def denoise_add_noise(x, t, pred_noise, z=None):
if z is None:
z = torch.randn_like(x)
noise = b_t.sqrt()[t] * z
mean = (x - pred_noise * ((1 - a_t[t]) / (1 - ab_t[t]).sqrt())) / a_t[t].sqrt()
return mean + noise # return sampling p(xt-1|xt)
def denoise_ddim(x, t, t_prev, pred_noise):
ab = ab_t[t]
ab_prev = ab_t[t_prev]
x0_pred = ab_prev.sqrt() / ab.sqrt() * (x - (1 - ab).sqrt() * pred_noise)
dir_xt = (1 - ab_prev).sqrt() * pred_noise
return x0_pred + dir_xt