A White Paper on Neural Network Quantization

发表于 |

A White Paper on Neural Network Quantization

  1. 高通白皮书

  2. Quantization fundamentals

    • basic block：y=Wx+b

    • 推理的瓶颈通常在带宽，32bit数据的加载和写入占据大部分能耗

    • 16个处理单元PE，使用int8可以优化数据瓶颈

    • 累加器Accumulator，通常保持32bit，做完加法以后再量化到8bit

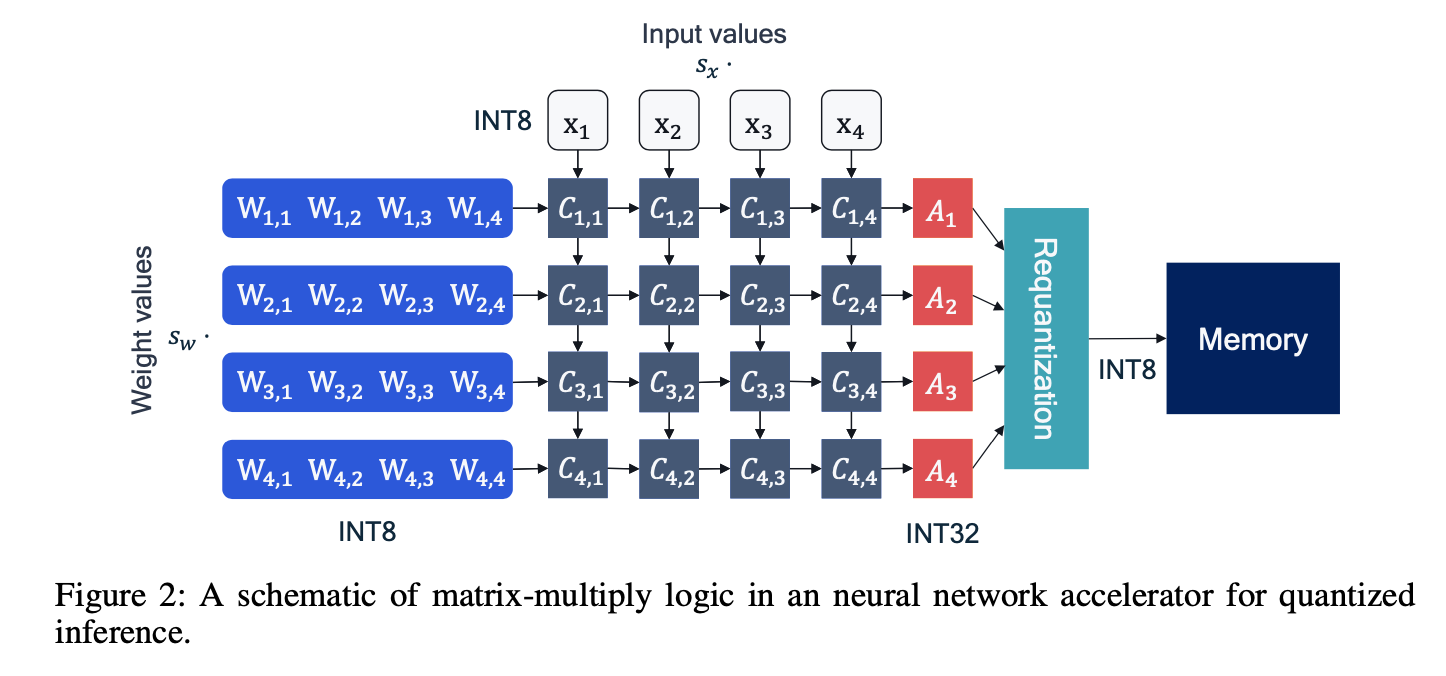
    • 浮点做定点近似：$\hat x=s_x x_{int} \approx x$

    • $\hat y = \hat b + \sum (s_w w_{int}) (s_x x_{int}) = \hat b + s_w s_x \sum(w_{int} x_{int})$

    • 常见的量化方式

      • 均匀仿射量化(Uniform affine quantization)，也叫非对称量化(asymmetric quantization)
        • 量化：$x_{int} = clamp(round[\frac{x}{s}]+z, 0, 2^{b}-1)$
        • 反量化：$x\approx \hat x=s(x_{int}-z)$
        • 反量化恢复的x范围：$[-sz，s(2^b-1-z)]$，不再这个范围内的值就被截断了，扩大s能够扩大量化范围减少clipping error，但是会增加rounding error，所以在截断误差和舍入误差之间需要trade-off
      • 对称均匀量化(Symmetric uniform quantization)
        • 省略zero point
        • 量化：$x_{int} = clamp (round[\frac{x}{s}], 0, 2^b-1)$
        • 反量化：$\hat x=sx_{int}$
        • 无符号对称量化非常适用于单边激活值，如relu
        • 有符号对称量化可以被用于大致关于零对称分布的数据（如conv-bn）
      • 二次幂量化(Power-of-two quantizer)
        • 二次幂量化是对称量化的一个特例，zero point依旧是0，比例因子被限制为二次幂
        • 可以提升硬件的计算效率
        • 但是比例因子s的限制性表达可能会使截断误差和舍入误差之间的权衡变得复杂

    • 量化粒度

      • per tensor量化：为每个tensor定义一组量化参数（权重量化参数$s_w, z_w$以及激活量化参数$s_x, z_x$）
      • per channel量化：
        • 对于权重量化，可以为每个输出通道指定一个不同的量化器，因为basic block里面是逐行累加，不会影响计算效率
        • 但是对于激活值量化，通常不会做per-channel量化，因为如果每个x都有一组s和z，$\sum wx$中的scale就没法提到$\sum$外面了
        • 实际卷积的per-channel量化，是对每个kernel单独统计一个scale和zero-point
          *
      • per group量化：还有比per channel更细粒度的量化方案，增加组的粒度通常可以提升量化的准确性，但是要额外付出一些计算开销，目前大多数的定点累加器都不支持这类操作

    • 量化模拟

      • 在训练硬件上模拟量化行为

        • 用于QAT
        • 用于测试神经网络在量化设备上的运行情况
        • on-device真实场景下：tensor、weight都是int8的
        • 模拟场景下：tensor、weights都是浮点的，通过给conv加入量化器来模拟权重的量化，通过给act加入量化器来模拟激活值的量化
        • 量化器实现了上面定义的量化函数

        • 量化器的输入输出都是浮点格式的，但是输出是限制在量化范围以内的

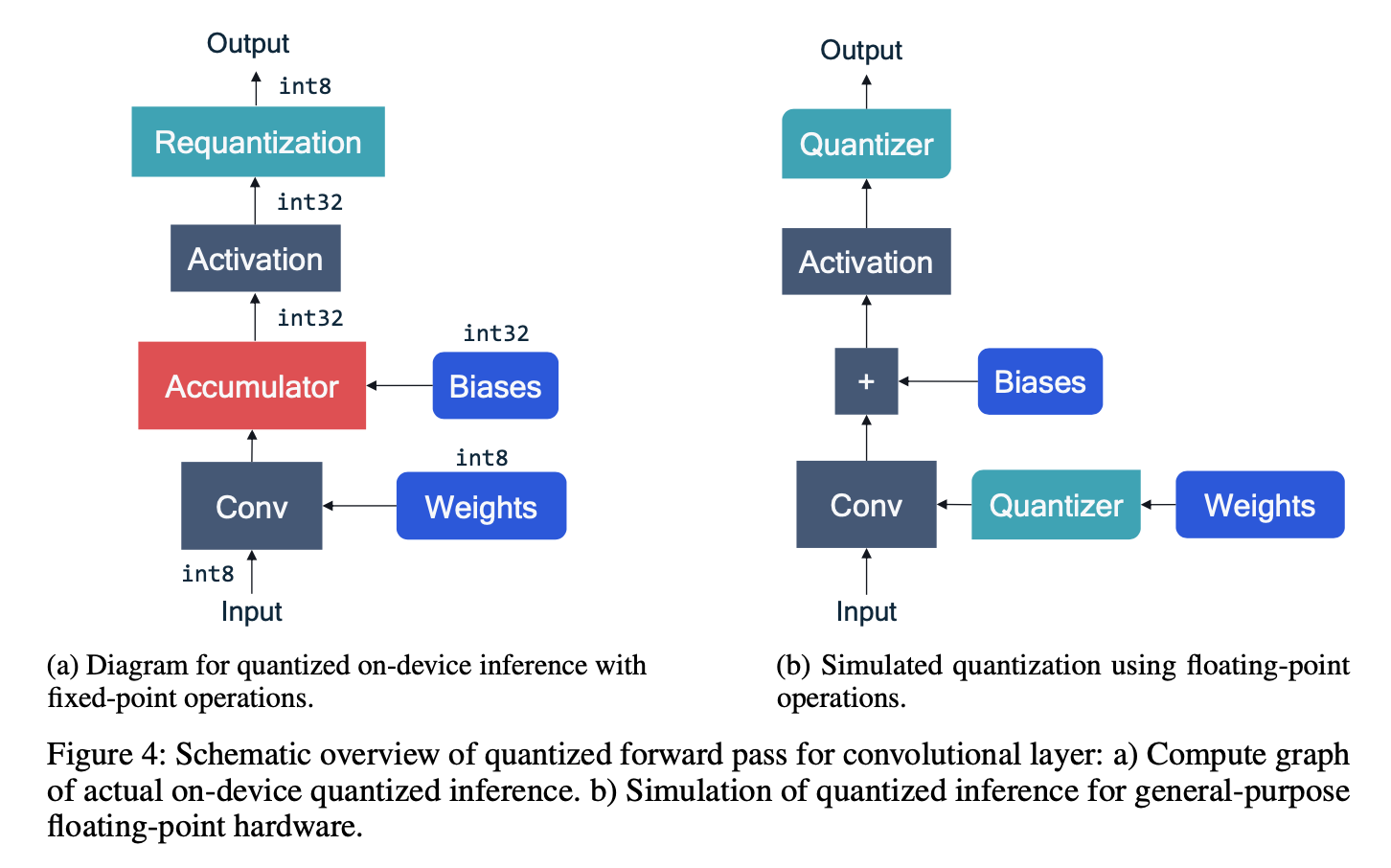
    • 常见层量化

      • 批量归一化的折叠(Batch normalization folding)：bn参数就被融合到前一个线性层
      • 激活函数融合(Activation function fusing)：
        • 通常我们做完conv-bn以后要反量化了，然后写入内存，然后act层再读取进来，再进行量化，然后process
        • 但是像relu可以和轻松的和反量化前的conv-bn结合：直接对量化值做relu就可以了，这样就节省了一组读写和量化
        • 像sigmoid/swish之类的，硬件会针对这个计算有专门的实现：泰勒展开近似/查找表
      • 最大值池化(Max pooling)：激活量化是不需要的，因为输入和输出的范围是一致的
      • 均值池化(Average pooling)：整数的平均不一定是整数，因此需要在平均之后增加一个量化步骤。但是我们对输入和输出使用相同的量化器，因为求平均不会显著改变量化后值的范围。
      • 逐点相加(Element-wise addition)：在计算的时候两个输入的量化范围必须要完全匹配。如果输入的量化范围不匹配，就需要格外的注意才能确保计算能正确的执行。因此没有公认的解决方案。额外增加一个反量化步骤可以粗略的模拟增加的误差或者噪声，另外一种方案是绑定多个输入的量化器从而实现一致的输入，这可以省去反量化步骤但是可能需要微调(fine-tuning)。
      • 连接(Concatenation)：被连接的两个分支通常不共享量化参数，这意味着它们的量化范围不一定会重叠，因此反量化步骤可能是需要的。与逐点相加一样，你可以对网络进行优化(fine-tuning)以使得多个连接分支可以共享量化参数。
      • 通常对激活使用非对称量化，对权重使用对称量化：因为权重分布通常在0附近，而且反量化WX时候不会引入running time item $s_wz_ws_xx_{int}$

  3. PTQ

    • data-free/small calibration set

  4. QAT

    • STE：直通估计器，bp时候跳过量化器，同时假定该模块的梯度为1，更新浮点参数以后，用min-max来更新量化器的s和z

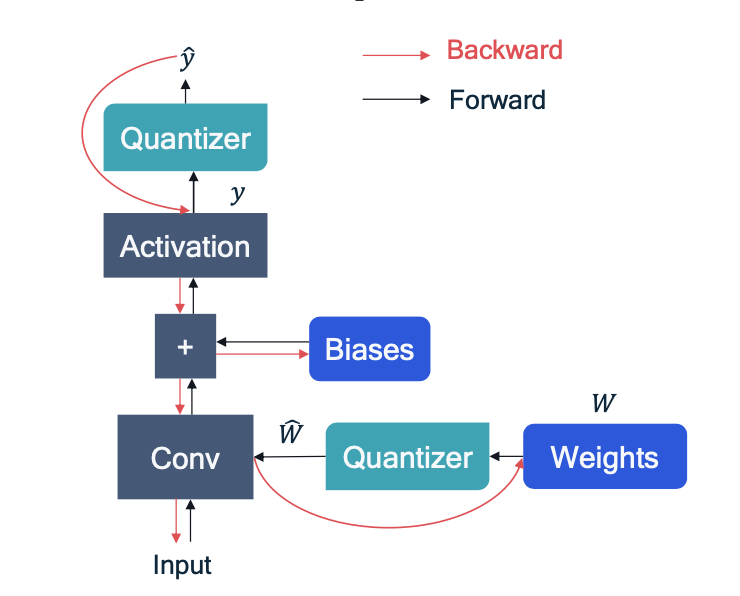
    • LSQ：可微量化参数，训练中对s和z求导，直接更新量化参数

    • standart QAT pipeline

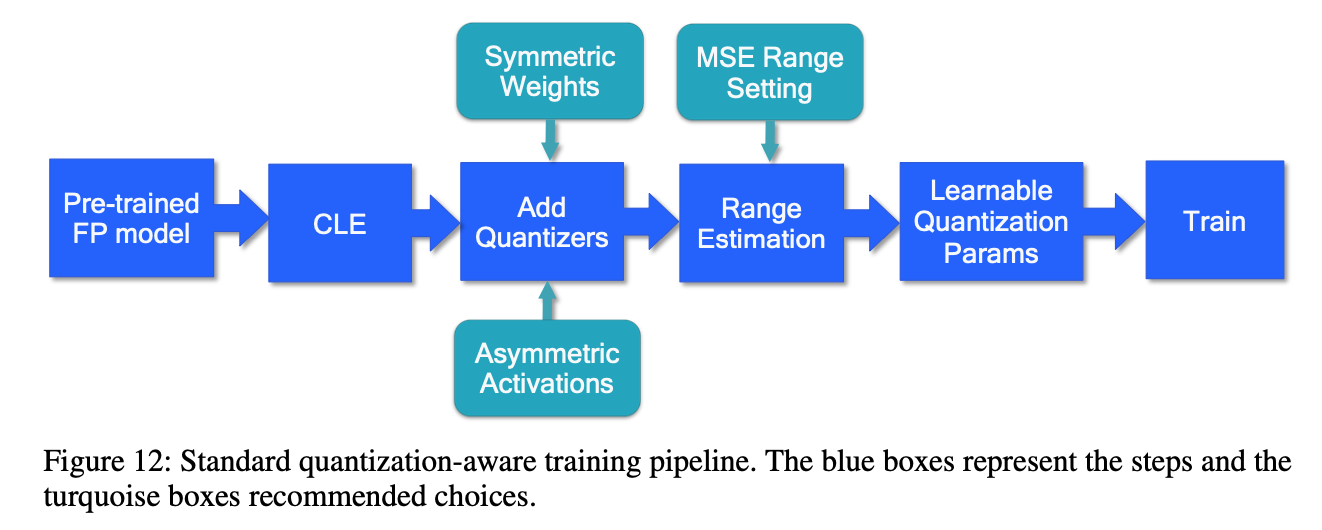
    • 首先拿到trained浮点模型

    • Cross-layer equalization 跨层均衡化(CLE) ，对于遇到不平衡权重分布的模型（例如 MobileNet 架构），此步骤是必要的。

    • Add quantizers 使用量化模块，选择量化器并在网络中添加量化操作，针对特定硬件，通常对权重使用对称量化器，对激活使用非对称量化器，如果硬件支持，对权重使用per-channel量化

    • Range estimation 范围设置，基于层的MSE标准来设置所有量化参数，在按通道(per-channel)量化的特定情况下，使用最小-最大设置有时可能是更有利的。

    • Learnable Quantization Parameters 量化参数可学习，直接学习量化参数，用对s和z的梯度直接更新他们