HMC: Hierarchical Multi-Label Classification Networks

发表于 |

ICML2018，multi-label，hierarchical

理想数据集的类别间是互斥的，但是现实往往存在层级/包含关系，多个数据集合并时也会有这个情况

reference code: https://github.com/Tencent/NeuralNLP-NeuralClassifier/blob/master/model/classification/hmcn.py

HMCN: Hierarchical Multi-Label Classification Networks

  1. 动机

    • HMC：hierarchical multi-label classification
      • classes are hierarchically structured，类别是有层级关系的
      • objects can be assigned to multiple paths，目标可能点亮多条tree path——多标签
    • application domains
      • text classification
      • image annotation
      • bioinformatics tasks such as protein function prediction
    • propose HMCN
      • local + global loss
      • local：discover local hierarchical class-relationships
      • global：global information from the entire class while penalizing hierarchical violations

  2. 论点

    • common methods
      • local-based：
        • 建立层级的top-down局部分类器，每个局部分类器用于区分当前层级，combine losses
        • computation expensive，更善于提取wordTree局部的信息，容易overfitting
      • global-based：
        • 只有一个分类器，将global structure associate起来
        • cheap，没有error-propagation problem，容易underfitting
    • our novel approach
      • combine两者的优点
      • recurrent / non-recurrent版本都有
      • 由multiple outputs构成
        • 每个class hierarchy level有一个输出：local output
        • 全局还有一个global output
      • also introduce a hierarchical violation penalty

  3. 方法

    • a feed-forward architecture (HMCN-F)

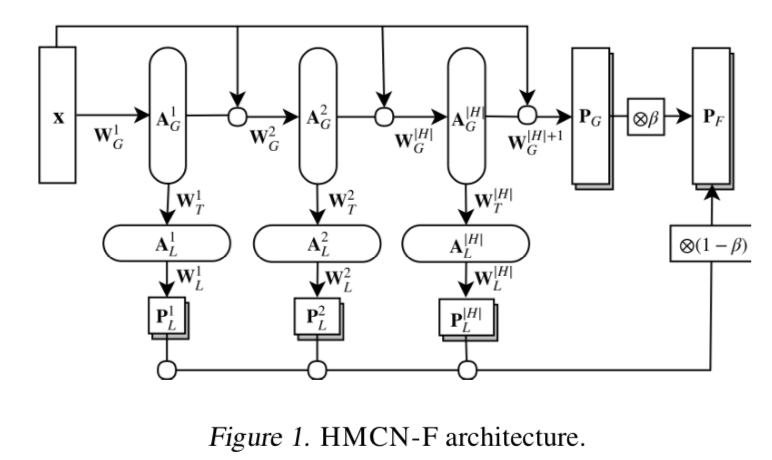
      • notations
        • feature vec $x \in R^{D}$：输入向量
        • $C^h$：每层的节点
        • $|H|$：总层数
        • $|C|$：总类数
      • global flow
        • 第一行横向的data flow
        • 将$i^{th}$层的信息carry到第$(i+1)^{th}$层
        • 第一层：$A_G^1 = \phi(W_G^1 x +b_G^1)$
        • 接下来的层：$A_G^h = \phi(W_G^h(A_G^{h-1} \odot x) +b_G^h)$
        • 最终的global prediction：$P_G=\sigma(W_G^{H+1}A_G^{H}+b_G^{H+1}) \in R^{|C|}$
      • local flow
        • start from 每个level的global hidden layer
        • local hidden layer：$A_L^h = \phi(W_T^hA_G^{h} +b_T^h)$
        • local prediction：$P_L^h = \sigma(W_L^hA_L^{h} +b_L^h) \in R^{C^h}$
      • merge information
        • 将local的prediction vectors concat起来
        • 然后和global preds相加
        • $P_F = \beta (P_L^1 \odot P_L^2 \odot… P_L^1) + (1-\beta) P_G$
      • hyperparams
        • $\beta=0.5$
        • fc-bn-dropout：dim=384，drop_rate=0.6

    • a recurrent architecture (HMCN-R)

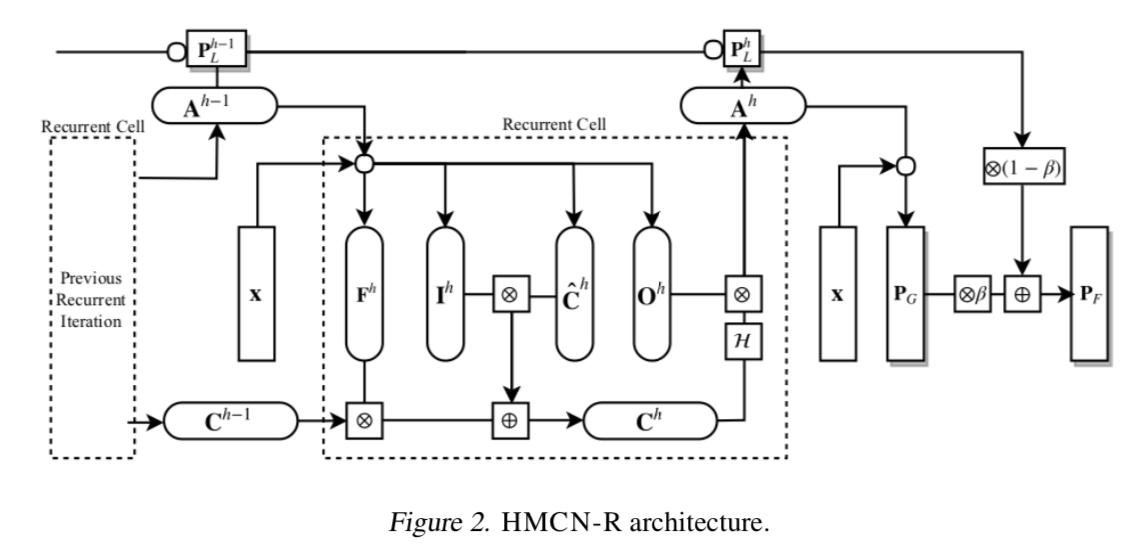
    • training details

      • small datasets with large number of classes
      • Adam
      • lr=1e-3

  4. 实验

    • 【小batch反而结果更好】one can achieve better results by training HMCN models with smaller batches

YOLO9000: 回顾yolov2的wordTree

  1. 动机

    • 联合训练，为了扩展类数
      • 检测样本梯度回传full loss
      • 分类样本只梯度回传分类loss

  2. Hierarchical classification

    • 构建WordTree

    • 对每个节点的预测是一个条件概率：$Pr(child_node|parent_node)$

    • 这个节点的绝对概率是整条链路的乘积

    • 每个样本的根节点概率$Pr(object)$是1

    • 对每个节点下面的所有children做softmax

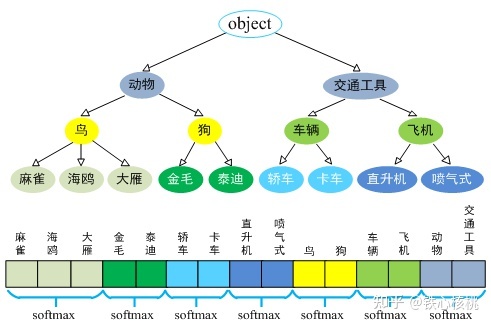
    • 首先论文就先用darknet19训了一个1369个节点的层次分类任务

      • 1000类flat softmax on ImageNet：72.9% top-1，91.2% top-5
      • 1369类wordTree softmax on ImageNet：71.9% top-1，90.4% top-5
      • 观察到Performance degrades gracefully：总体精度下降很少，而且即使分不清是什么狗品种，狗这一类的概率还是能比较高

    • 然后用在检测上

      • 每个目标框的根节点概率$Pr(object)$是yolo的obj prob
      • 仍旧对每个节点做softmax，标签是高于0.5的最深节点，不用连乘条件概率
        • take the highest confidence path at every split
        • until we reach some threshold
        • and we predict that object class
      • 对一个分类样本
        • 我们用全图类别概率最大的bounding box，作为它的分类概率
        • 然后还有objectness loss，预测的obj prob用0.3IOU来threshold：即如果这个bnd box的obj prob<0.3是要算漏检的