L2 Regularization and Batch Norm

reference：

解释了之前的一个疑点：

在keras自定义的BN层中，没有类似kernel_regularizer这样的参数
在我们写自定义optmizer的时候，BN层也不进行weight decay的

L2 Regularization versus Batch and Weight Normalization

动机
- 两个common tricks：Normalization（BN、WN、LN等）和L2 Regularization
  - 发现两者结合时L2 regularization对normalization层没有正则效果
  - L2 regularization反而对norm layer的scale有影响，间接影响了learning rate
  - 现代优化器如Adam只能间接消除这种影响
论点
- BN
  - popular in training deep networks
  - solve the problem of covariate shift
  - 使得每个神经元的输入保持normal分布，加速训练
  - mean & variance：training time基于每个mini-batch计算，test time使用所有iteration的mean & variance的EMA
- usually trained with SGD with L2 regularization
  - result in weight decay：从数学表示上等价于对权重做衰减
  - 每一步权重scaled by a 小于1的数
  - 但是normalization strategies是对scale of the weights invariant的，因为在输入神经元之前都会进行norm
  - therefore
    - there is no regularizing effect
    - rather strongly influence the learning rate??👂
L2 Regularization
- formulation：
  - 在loss的基础上加一个regularization term，$L_{\lambda}(w)=L(w)+\lambda ||w||^2_2$
  - loss是每个样本经过一系列权重运算，$L(w)=\sum_N l_i (y(X_i;w,\gamma,\beta))$
  - 当使用normalization layer的时候：$y(X_i;w,\alpha,\beta)=y(X_i;\alpha w,\gamma,\beta)$，即loss term不会变
  - $L_{\lambda}(\alpha w)=L(w)+\lambda||w||^2_2$
  - 在有normalization layer的时候，L2 penalty还是能够通过reg term force权重的scale越来越小，但是不会影响优化进程（不影响main objective value），因为loss term不变
- Effect of the Scale of Weights on Learning Rate
  - BN层的输出是scale invariant的，但是梯度不是，梯度是成反比被抑制的！
  - 所以weights在变小，同时梯度在变大！
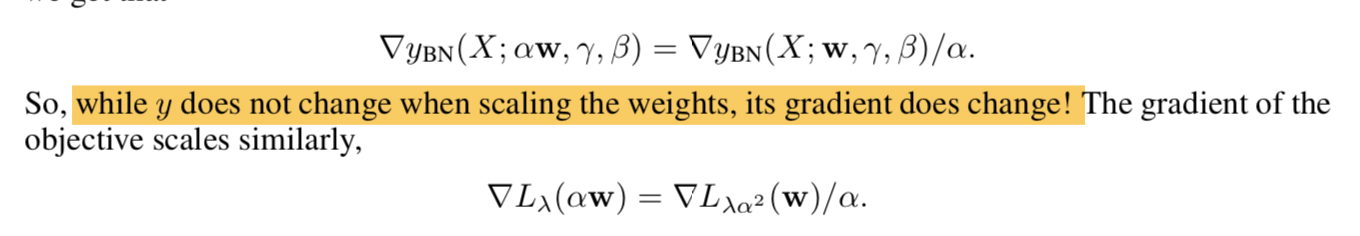
  - 在减小weight scale的时候，网络的梯度会变大，等价于学习率在变大，会引起震荡不稳定
  - 所以在设定hyper的时候，如果我们要适当加大weight decay $\lambda$，就要反比scale学习率
- Effect of Regularization on the Scale of Weights
  - during training the scale of weights will change
    - the gradients of the loss function will cause the norm of the weights to grow
    - the regularization term causes the weights to shrink