GHM

发表于 |

families:

  • [class-imbalanced CE]
  • [focal loss]
  • [generalized focal loss] focal loss(CE)的连续版本
  • [ohem]

keras implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
def weightedCE_loss(y_true, y_pred):
		alpha = .8
		pt = K.abs(y_true-y_pred)
		# clip
    pt = K.clip(pt, K.epsilon(), 1-K.epsilon())
    # ce
    ce = -K.log(1.-pt)
    # pos/neg reweight
    wce = tf.where(y_true>0.5, alpha* , (1-alpha)* )
    return wce

def focal_loss(y_true, y_pred):
		alpha = .25
		gamma = 2
		
		pt = K.abs(y_true-y_pred)
		# clip
    pt = K.clip(pt, K.epsilon(), 1-K.epsilon())
    # easy/hard reweight
		fl = -K.pow(pt, gamma) * K.log(1.-pt)
    # pos/neg reweight
    fl = tf.where(y_true>0.5, alpha*fl, (1-alpha)*fl)
    return fl
  
 def generalized_focal_loss(y_true, y_pred):
		# CE = -ytlog(yp)-(1-yt)log(1-yp)
  	# GFL = |yt-yp|^beta * CE
    beta = 2
    # clip y_pred
    y_pred = K.clip(y_pred, K.epsilon(), 1-K.epsilon())
    # ce
    ce = -y_true*K.log(y_pred) - (1-y_true)*K.log(1-y_pred)   # [N,C]
    # easy/hard reweight
    gfl = K.pow(K.abs(y_true-y_pred), beta) * ce
    return gfl

def ce_ohem(y_true, y_pred):
  	pt = K.abs(y_true-y_pred)
		# clip
    pt = K.clip(pt, K.epsilon(), 1-K.epsilon())
    # ce
    ce = -K.log(1.-pt)
    # sort loss
    k = 50
    ohem_loss, indices = tf.nn.top_k(ce, k=k)   # topk loss: [k,], topk indices: [k,], idx among 0-b
    mask = tf.where(ce>=ohem_loss[k-1], tf.ones_like(ce), tf.zeros_like(ce))
    return mask*ce

Gradient Harmonized Single-stage Detector

  1. 动机

    • one-stage detector
      • 核心challenge就是imbalance issue
      • imbalance between positives and negatives
      • imbalance between easy and hard examples
      • 这两项都能归结为对梯度的作用：a term of the gradient
    • we propose a novel gradient harmonizing mechanism (GHM)
      • balance the gradient flow
      • easy to embed in cls/reg losses like CE/smoothL1
      • GHM-C for anchor classification
      • GHM-R for bounding box refinement
    • proved substantial improvement on COCO
      • 41.6 mAP
      • surpass FL by 0.8

  2. 论点

    • imbalance issue

      • easy and hard：

        • OHEM
        • directly abandon examples
        • 导致训练不充分

      • positive and negative

        • focal loss
        • 有两个超参，跟data distribution绑定
        • not adaptive

      • 通常正样本既是少量样本又是困难样本，而且可以通通归结为梯度分布不均匀的问题

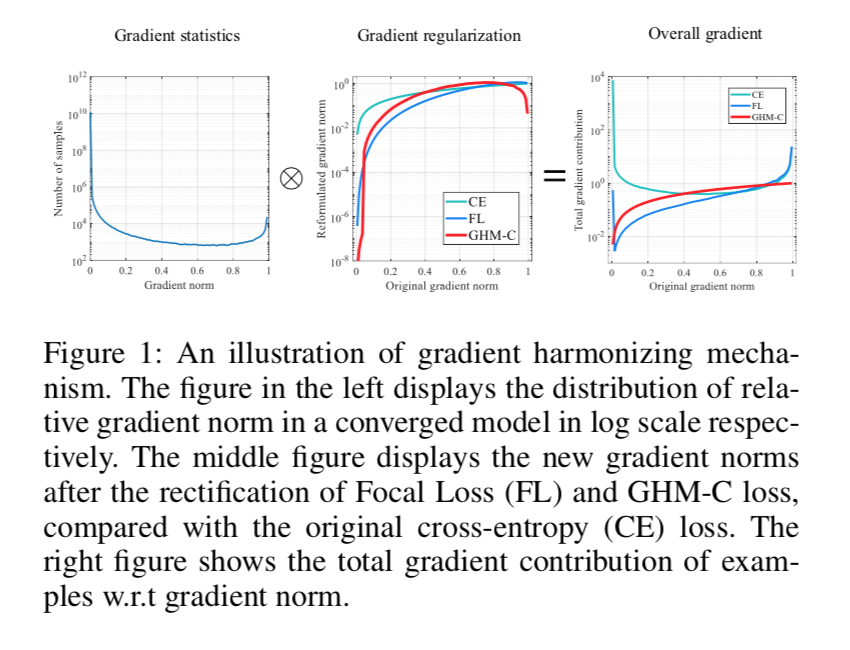
        • 大量样本只贡献很小的梯度，通常对应着大量负样本，总量多了也可能会引导梯度（左图）
        • hard样本要比medium样本数量大，我们通常将其看作离群点，因为模型稳定以后这些hard examples仍旧存在，他们会影响模型稳定性（左图）
        • GHM的目标就是希望不同样本的gradient contribution保持harmony，相比较于CE和FL，简单样本和outlier的total contribution都被downweight，比较harmony（右图）

    • we propose gradient harmonizing mechanism (GHM)

      • 希望不同样本的gradient contribution保持harmony
      • 首先研究gradient density，按照梯度聚类样本，并相应reweight
      • 针对分类和回归设计GHM-C loss和GHM-R loss
      • verified on COCO
        • GHM-C比CE好得多，sligtly better than FL
        • GHM-R也比smoothL1好
        • attains SOTA
      • dynamic loss：adapt to each batch

  3. 方法

    • Problem Description

      • define gradient norm $g = |p - p^*|$

      • the distribution g from a converged model

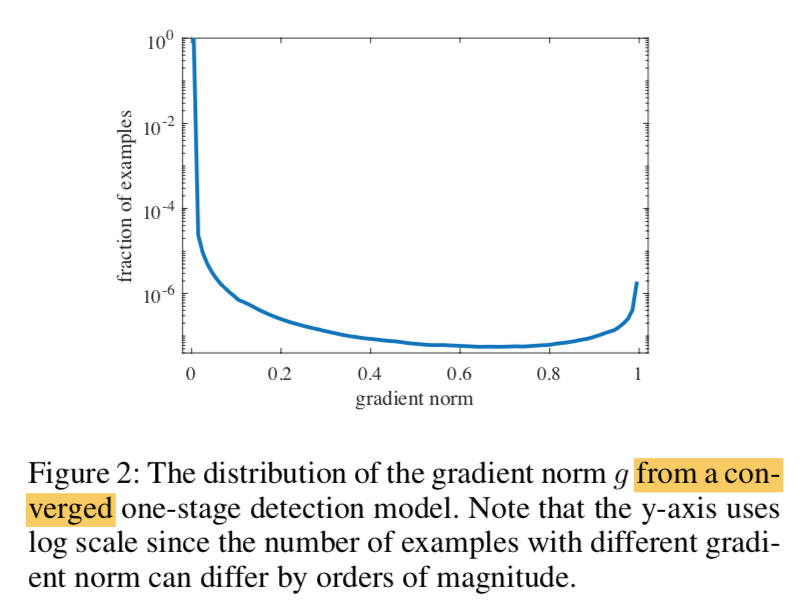
        • easy样本非常多，不在一个数量级，会主导global gradient
        • 即使收敛模型也无法handle一些极难样本，这些样本梯度与其他样本差异较大，数量还不少，也会误导模型

    • Gradient Density

      • define gradient density $GD(g) = \frac{1}{l_{\epsilon}(g)} \sum_{k=1} \delta_{\epsilon}(g_k,g)$
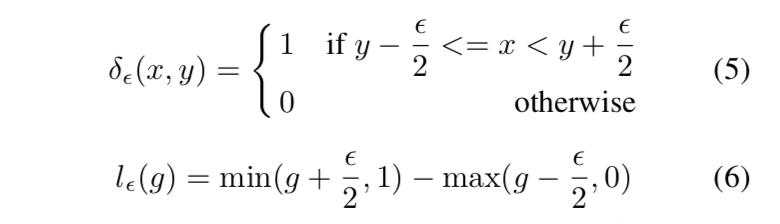
        • given a gradient value g
        • 统计落在中心value为$g$，带宽为$\epsilon$的范围内的梯度的样本量
        • 再用带宽去norm
      • define the gradient density harmony parameter $\beta_i = \frac{N}{GD(g_i)}$
        • N是总样本量
        • 其实就是与density成反比
        • large density对应样本会被downweight

    • GHM-C Loss

      • 将harmony param作为loss weight，加入现有loss

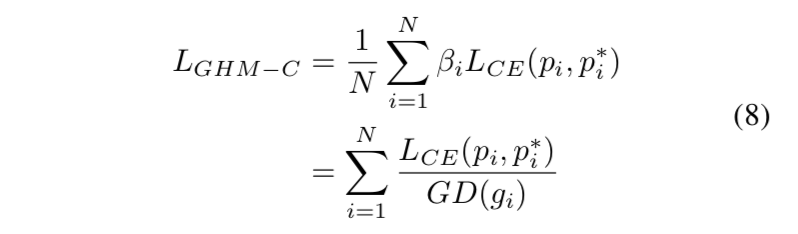
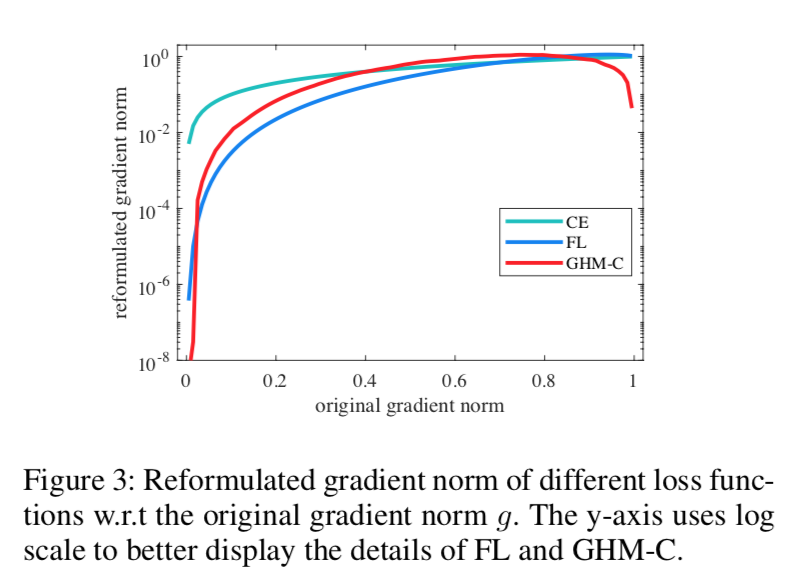
        • 可以看到FL主要压简单样本（基于sample loss），GHM两头压（基于sample density）
        • 最终harmonize the total gradient contribution of different density group
        • dynamic wrt mini-batch：使得训练更加efficient和robust

      • Unit Region Approximation

        • 将gradient norm [0,1]分解成M个unit region
        • 每个region的宽度$\epsilon = \frac{1}{M}$
        • 落在每个region内的样本数计作$R_{ind(g)}$，$ind(g)$是g所在region的start idx
        • the approximate gradient density：$\hat {GD}(g) = \frac{R_{ind(g)}}{\epsilon} =R_{ind(g)}M $

        • approximate harmony parameter & loss：

          • we can attain good performance with quite small M
          • 一个密度区间内的样本可以并行计算，计算复杂度O(MN)

      • EMA

        • 一个mini-batch可能是不稳定的
        • 所以通过历史累积来更新维稳：SGDM和BN都用了EMA
        • 现在每个region里面的样本使用同一组梯度，我们对每个region的样本量应用了EMA
          • t-th iteraion
          • j-th region
          • we have $R_j^t$
          • apply EMA：$S_j^t = \alpha S_j^(t-1) + (1-\alpha )R_j^t$
          • $\hat GD(g) = S_{ind(g)} M$
        • 这样gradient density会更smooth and insensitive to extreme data

    • GHM-R loss

      • smooth L1：

        • 通常分界点设置成$\frac{1}{9}$
        • SL1在线性部分的导数永远是常数，没法去distinguishing of examples
        • 用$|d|$作为gradient norm则存在inf

      • 所以先改造smooth L1：Authentic Smooth L1

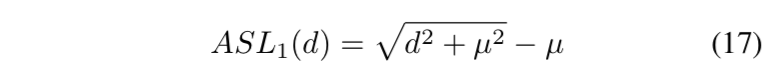
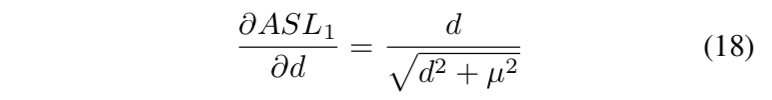
        • $\mu=0.02$
        • 梯度范围正好在[0,1)

      • define gradient norm as $gr = |\frac{d}{\sqrt{d^2+\mu^2}}|$

        • 观察converged model‘s gradient norm for ASL1，发现大量是outliers

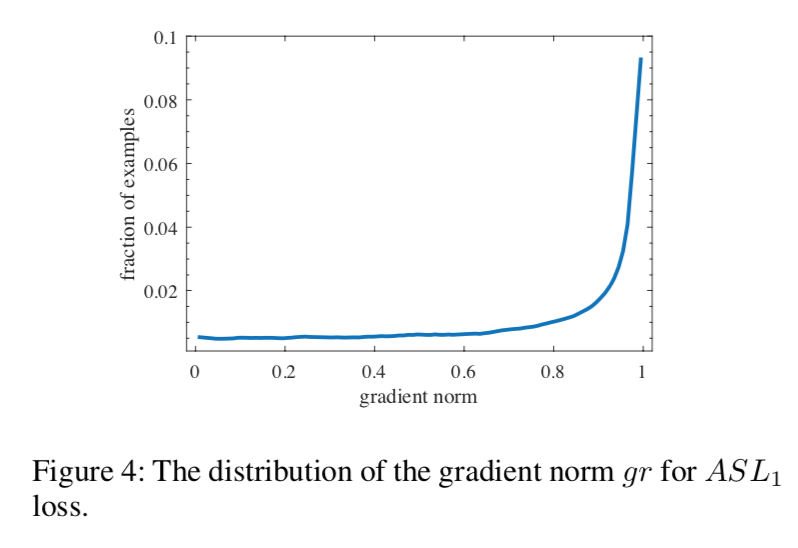
        • 同样用gradient density进行reweighting

        • 收敛状态下，不同类型的样本对模型的gradient contribution

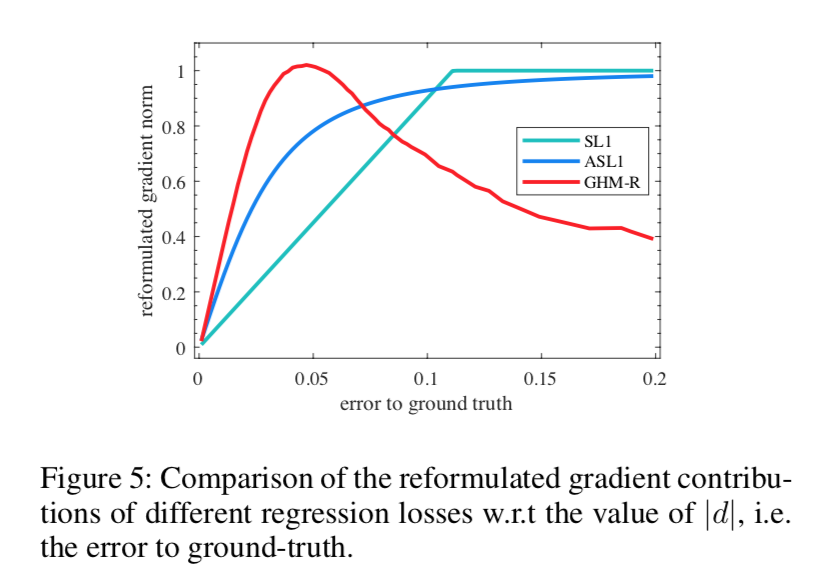
          • regression是对所有正样本进行计算，主要是针对离群点进行downweighting
          • 这里面的一个观点是：在regression task里面，并非所有easy样本都是不重要的，在分类task里面，easy样本大部分都是简单的背景类，但是regression分支里面的easy sample是前景box，而且still deviated from ground truth，仍旧具有充分的优化价值
          • 所以GHM-R主要是upweight the important part of easy samples and downweight the outliers

  4. 实验