[papers]
- [MLP-Mixer] MLP-Mixer: An all-MLP Architecture for Vision,Google
- [ResMLP] ResMLP: Feedforward networks for image classification with data-efficient training,Facebook
[references]
https://mp.weixin.qq.com/s/8f9yC2P3n3HYygsOo_5zww
MLP-Mixer: An all-MLP Architecture for Vision
动机
- image classification task
- neither of [CNN, attention] are necessary
- our proposed MLP-Mixer
- 仅包含multi-layer-perceptrons
- independently to image patches
- repeated applied across either spatial locations or feature channels
- two types
- applied independently to image patches
- applied across patches
方法
overview
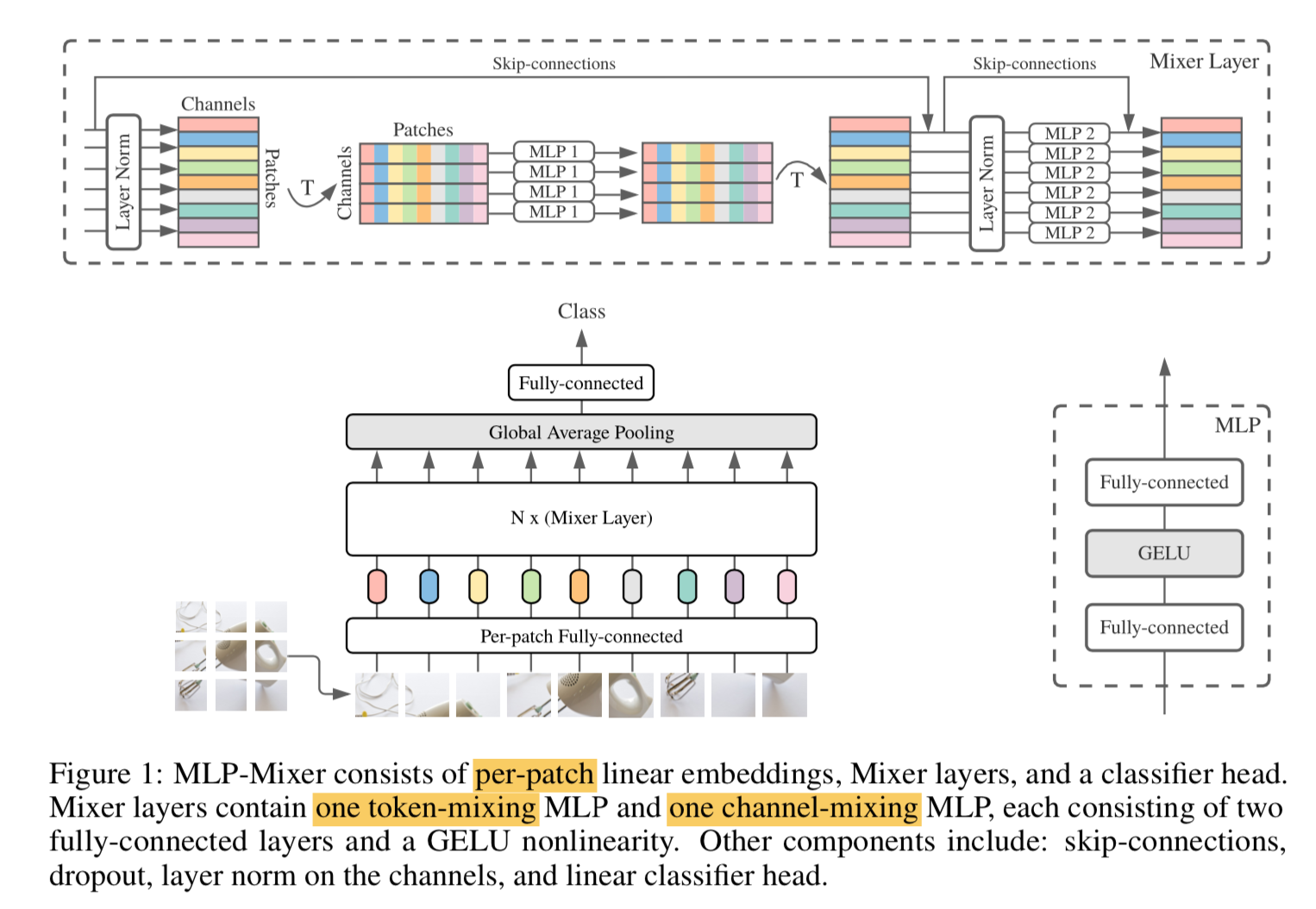
- 输入是token sequences
- non-overlapping image patches
- linear projected to dimension C
- Mixer Layer
- maintain the input dimension
- channel-mixing MLP
- operate on each token independently
- 可以看作是1x1的conv
- token-mixing MLP
- operate on each channel independently
- take each spatial vectors (hxw)x1 as inputs
- 可以看作是一个global depth-wise conv,s1,same pad,kernel size是(h,w)
- 最后对token embedding做GAP,提取sequence vec,然后进行类别预测
- 输入是token sequences
idea behind Mixer
- clearly separate the per-location operations & cross-location operations
- CNN是同时进行这俩的
- transformer的MSA同时进行这俩,MLP只进行per-location operations
Mixer Layer
two MLP blocks
given input $X\in R^{SC}$,S for spatial dim,C for channel dim
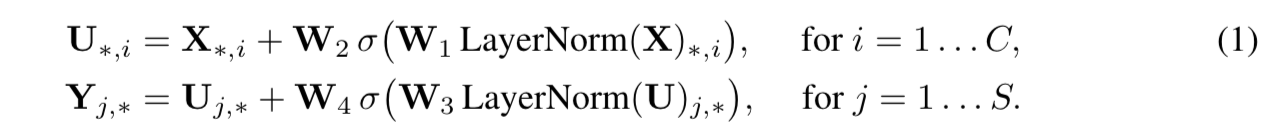
先是token-mixing MLP
- acts on S dim
- maps $R^S$ to $R^S$
- share across C-axis
- LN-FC-GELU-FC-residual
然后是channel-mixing MLP
- acts on C dim
- maps $R^C$ to $R^C$
- share across S-axis
- LN-FC-GELU-FC-residual
fixed width,更接近transformer/RNN,而不是CNN那种金字塔结构
不使用positional embeddings
- the token-mixing MLPs are sensitive to the order of the input tokens
- may learn to represent locations
实验
ResMLP: Feedforward networks for image classification with data-efficient training
动机
- entirely build upon MLP
- alternates from a simple residual network
- a linear layer to interact with image patches
- a two-layer FFN to interact independently with each patch
- affine transform替代LN是一个特别之处
- trained with modern strategy
- heavy data-augmentation
- optionally distillation
- show good performace on ImageNet classification
论点
- strongly inspired by ViT but simpler
- 没有attention层,只有fc层+gelu
- 没有norm层,因为much more stable to train,但是用了affine transformation
- strongly inspired by ViT but simpler
方法
overview
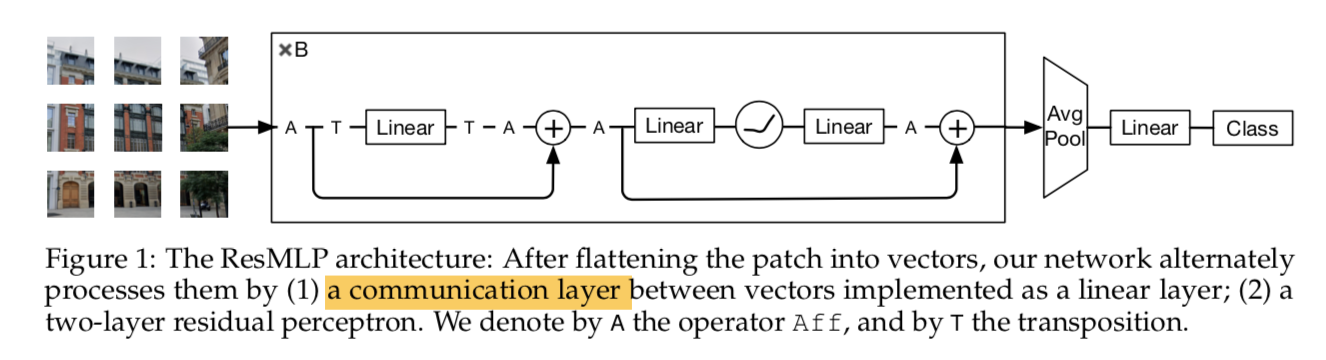
- takes flattened patches as inputs
- typically N=16:16x16
- linear project the patches into embeddings
- form $N^2$ d-dim embeddings
- ResMLP Layer
- main the dim throughout $[N^2,d]$
- a simple linear layer
- interaction between the patches
- applied to all channels independently
- 类似depth-wise conv with global kernel的东西,线性!!
- a two-layer-mlp
- fc-GELU-fc
- independently applied to all patches
- 非线性!!
- average pooled $[d-dim]$ + linear classifier $cls-dim$
- takes flattened patches as inputs
Residual Multi-Layer Perceptron Layer
- a linear layer + a FFN layer
- each layer is paralleled with a skip-connection
没用LN,但是用了learnable affine transformation
- $Aff_{\alpha, \beta} (x) = Diag(\alpha) x + \beta$
- rescale and shifts the input component-wise:对每个patch,分别做affine变换
- 在推理阶段可以与上一层线性层合并:no cost
- 用了两次
- 第一个用在main path上用来替代LN:初值为identity transform(1,0)
- 第二个在residual path里面,down scale to boost,用一个small value初始化
given input: $d\times N^2$ matrix $X$
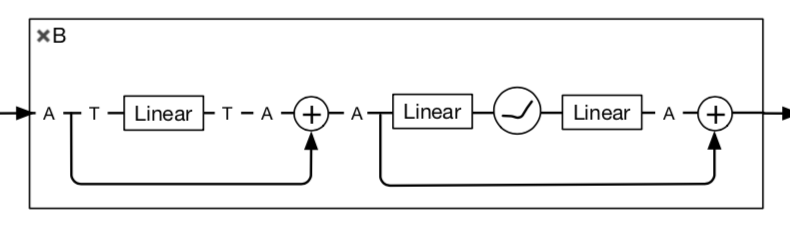
- affine在d-dim上做
- 第一个Linear layer在$N^2-dim$上做:参数量$N^2 \times N^2$
第二、三个Linear layer在$d-dim$上做:参数量$d \times 4d$ & $4d \times d$