memory bank

发表于 |

Unsupervised Feature Learning via Non-Parametric Instance Discrimination

  1. 动机

    • unsupervised learning
      • can we learn good feature representation that captures apparent similarity among instances instead of classes
      • formulate a non-parametric classification problem at instance-level
      • use noise contrastive estimation
    • our non-parametric model
      • highly compact：128-d feature per image，only 600MB storage in total
      • enable fast nearest neighbour retrieval
    • 【QUESTION】无类别标签，单靠similarity，最终的分类模型是如何建立的？
    • verified on
      • ImageNet 1K classification
      • semi-supervised learning
      • object detection tasks

  2. 论点

    • observations
      • ImageNet top-5 err远比top-1 err小
      • second highest responding class is more likely to be visually related
      • 说明模型隐式地学到了similarity
      • apparent similarity is learned not from se- mantic annotations, but from the visual data themselves
    • 将class-wise supervision推到一个极限
      • 就变成了instance-level
      • 类别数变成了the whole training set：softmax to many more classes becomes infeasible
        • approximate the full softmax distribution with noise-contrastive estimation(NCE)
        • use a proximal regularization to stablize the learning process
    • train & test
      • 通常的做法是learned representations加一个线性分类器
      • e.g. SVM：但是train和test的feature space是不一致的
      • 我们用了KNN：same metric space

  3. 方法

    • overview

      • to learn a embedding function $f_{\theta}$
      • distance metric $d_{\theta}(x,y) = ||f_{\theta}(x)-f_{\theta}(y)||$
      • to map visually similar images closer

      • instance-level：to distinct between instances

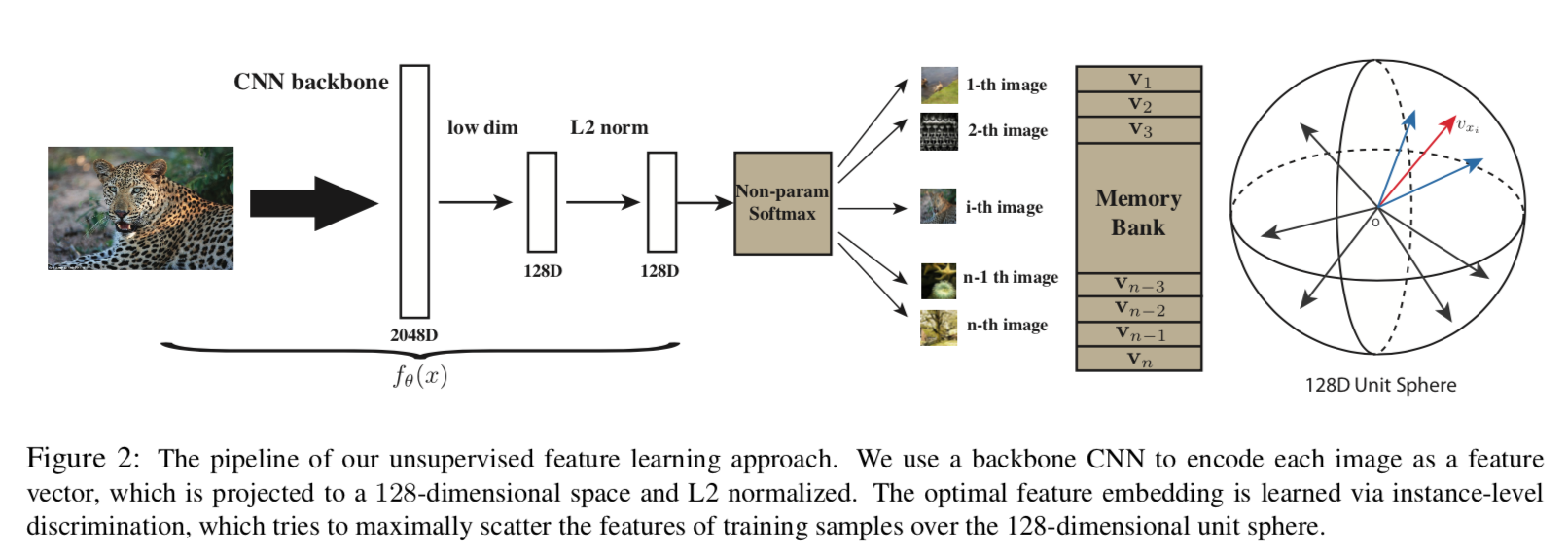
    • Non-Parametric Softmax Classifier

      • common parametric classifier

        • given网络预测的N-dim representation $v=f_{\theta}(x)$
        • 要预测C-classes的概率，需要一个$W^{NC}$的projection：$P(i|v) = \frac{exp (W^T_iv)}{\sum exp (W^T_jv)}$

      • Non-Parametric version

        • enforce $||v||=1$ via L2 norm
        • replace $W^T$ with $v^T$
        • then the probability：$P(i|v) = \frac{exp (v^T_iv/\tau)}{\sum exp (v^T_jv / \tau)}$
        • temperature param $\tau$：controls the concentration level of the distribution

        • the goal is to minimize the negative log-likelihood

        • 意义：L2 norm将所有的representation映射到了一个128-d unit sphere上面，$v_i^T v_j$度量了两个projection vec的similarity，我们希望同类的vec尽可能重合，不同类的vec尽可能正交

          • class weights $W$ are not generalized to new classes
          • but feature representations $V$ does

      • memory bank

        • 因为是instance level，C-classes对应整个training set，也就是说${v_i}$ for all the images are needed for loss
        • Let $V={v_i}$ 表示memory bank，初始为unit random vectors
        • every learning iterations
          • $f_\theta$ is optimized by SGD
          • 输入$x_i$所对应的$f_i$更新到$v_i$上
          • 也就是只有mini-batch中包含的样本，在这一个step，更新projection vec

    • Noise-Contrastive Estimation

      • non-parametric softmax的计算量随着样本量线性增长，millions level样本量的情况下，计算太heavy了

      • we use NCE to approximate the full softmax

      • assume

        • noise samples的uniform distribution：$P_n =\frac{1}{n}$
        • noise samples are $m$ times frequent than data samples

      • 那么sample $i$ matches vec $v$的后验概率是：$h(i,v)=\frac{P(i|v)}{P(i|v)+mP_n}$

        • approximated training object is to minimize the negative log-likelihood of $h(i,v)$

      • normalizing constant $Z$的近似

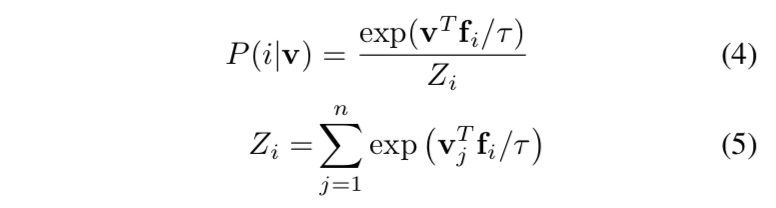
        • 主要就是分母这个$Z_i$的计算比较heavy，我们用Monte Carlo采样来近似：

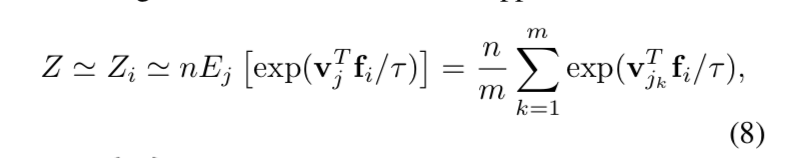
        • ${j_k}$ is a random subset of indices：随机抽了memory bank的一个子集来approx全集的分母，实验发现取batch size大小的子集就可以，m=4096

    • Proximal Regularization

      • the learning process oscillates a lot

        • we have one instance per class
        • during each training epoch each class is only visited once

      • we introduce an additional term

        • overall workflow：在每一个iteration t，feature representation是$v_i^t=f_{\theta}(x_i)$，而memory bank里面的representations来自上一个iteration step $V={v^{t-1}}$，我们从memory bank里面采样，并计算NCE loss，然后bp更新网络权重，然后将这一轮fp的representations update到memory bank的指定样本上，然后下一轮
        • 可以发现，在初始random阶段，梯度更新会比较快而且不稳定

        • 我们给positive sample的loss上额外加了一个$\lambda ||v_i^t-v_i^{t-1}||^2_2$，有点类似weight decay那种东西，开始阶段l2 loss会占主导，引导网络收敛

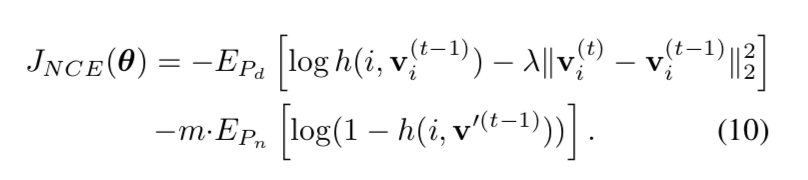
        • stabilize

        • speed up convergence
        • improve the learned representations

    • Weighted k-Nearest Neighbor Classifier

      • a test time，先计算feature representation，然后跟memory bank的vectors分别计算cosine similarity $s_i=cos(v_i, f)$，选出topk neighbours $N_k$，然后进行weighted voting
      • weighted voting：
        • 对每个class c，计算它在topk neighbours的total weight，$w_c =\sum_{i \in N_k} \alpha_i 1(c_i=c)$
        • $\alpha_i = exp(s_i/\tau)$
      • k = 200
      • $\tau = 0.07$