0. overview
keywords:SGD, moment, Nesterov, adaptive, ADAM, Weight decay
- 优化问题Optimization
- to minimize目标函数
- grandient decent
- gradient
- numerical:数值法,approx,slow
- analytical:解析法,exact,fast
- Stochastic
- 用minibatch的梯度来approximate全集
- $\theta_{k+1} = \theta_k - v_{t+1}(x_i,y_i)$
- classic optimizers:SGD,Momentum,Nesterov‘s momentum
- adaptive optimizers:AdaGrad,Adadelta,RMSProp,Adam
- gradient
- Newton
- modern optimizers for large-batch
- AdamW
- LARS
- LAMB
common updating steps
for current step t:
step1:计算直接梯度,$g_t = \nabla f(w_t)$
step2:计算一阶动量和二阶动量,$m_t \& V_t$
step3:计算当前时刻的下降梯度,$\eta_t = \alpha m_t/\sqrt {V_t}$
step4:参数更新,$w_{t+1} = w_t - \eta_t$
- 各种优化算法的主要差别在step1和step2上
滑动平均/指数加权平均/moving average/EMA
- 局部均值,与一段时间内的历史相关
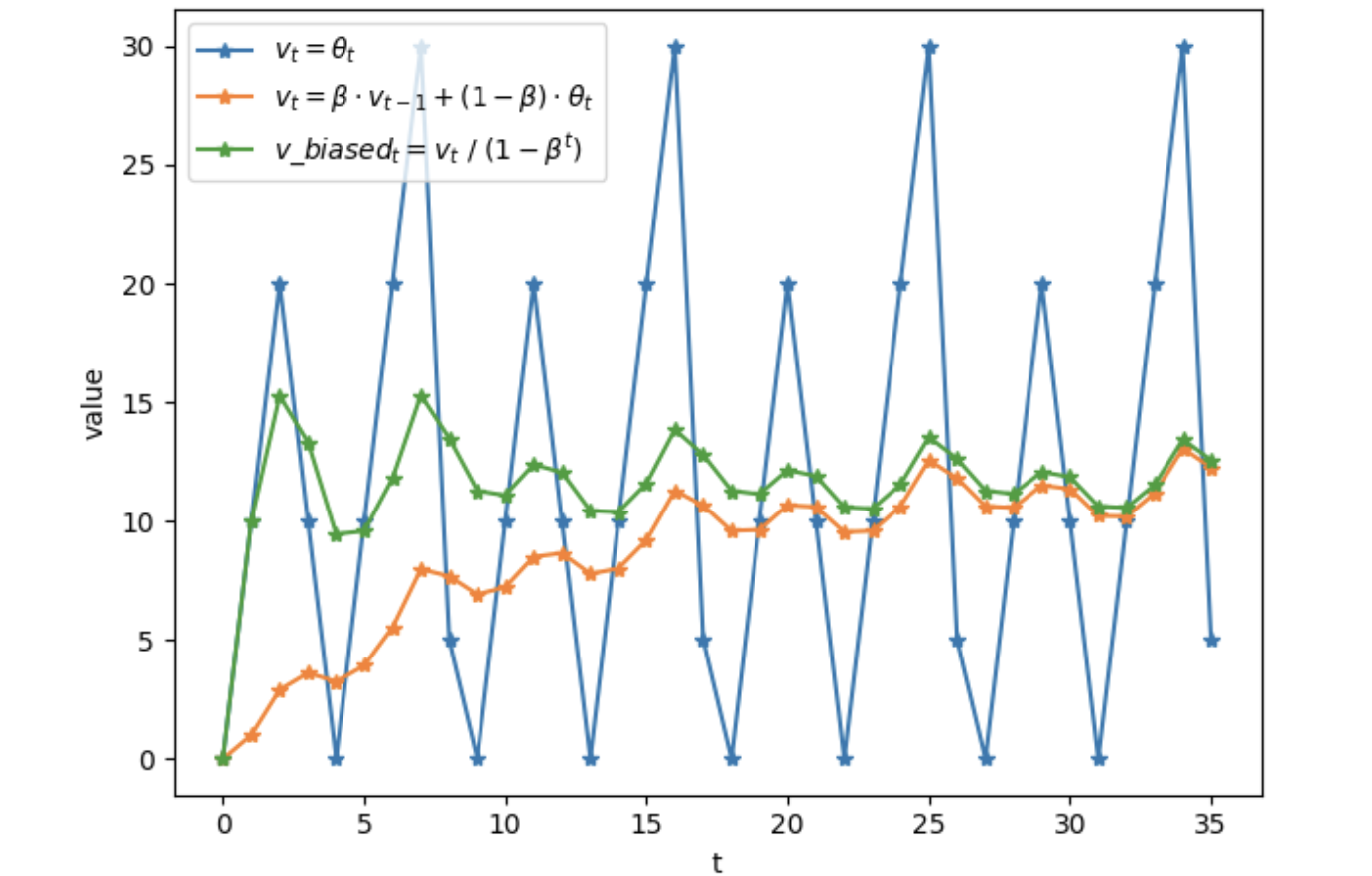
- $v_t = \beta v_{t-1}+(1-\beta)\theta_t$,大致等于过去$1/(1-\beta)$个时刻的$\theta$的平均值,但是在起始点附近偏差较大
- $v_{tbiased} = \frac{v_t}{1-\beta^t}$,做了bias correction
- t越大,越不需要修正,两个滑动均值的结果越接近
优缺点:不用保存历史,但是近似
SGD
- SGD没有动量的概念,$m_t=g_t$,$V_t=I^2$,$w_{t+1} = w_t - \alpha g_t$
- 仅依赖当前计算的梯度
- 缺点:下降速度慢,可能陷在local optima上持续震荡
SGDW (with weight decay)
- 在权重更新的同时进行权重衰减
- $w_{t+1} = (1-\lambda)w_t - \alpha g_t$
- 在SGD form的优化器中weight decay等价于在loss上L2 regularization
- 但是在adaptive form的优化器中是不等价的!!因为historical func(ERM)中regularizer和gradient一起被downscale了,因此not as much as they would get regularized in SGDW
SGD with Momentum
- 引入一阶动量,$m_t = \beta_1 m_{t-1} + (1-\beta_1) g_t$,使用滑动均值,抑制震荡
- 梯度下降的主要方向是此前累积的下降方向,略微向当前时刻的方向调整
SGD with Nesterov Acceleration
- look ahead SGD-momentum
- 在local minima的时候,四周没有下降的方向,但是如果走一步再看,可能就会找到优化方向
- 先跟着累积动量走一步,求梯度:$g_t = \nabla f(w_t-\alpha m_{t-1}/\sqrt {V_{t-1}})$
- 用这个点的梯度方向来计算滑动平均,并更新梯度
Adagrad
- 引入二阶动量,开启“自适应学习率”,$V_t = \sum_0^t g_k^2$,度量历史更新频率
- 对于经常更新的参数,我们已经积累了大量关于它的知识,不希望被单个样本影响太大,希望学习速率慢一些;对于偶尔更新的参数,我们了解的信息太少,希望能从每个偶然出现的样本身上多学一些,即学习速率大一些
- $\eta_t = \alpha m_t / \sqrt{V_t}$,本质上为每个参数,对学习率分别rescale
- 缺点:二阶动量单调递增,导致学习率单调衰减,可能会使得训练过程提前结束
AdaDelta/RMSProp
- 参考momentum,对二阶动量也计算滑动平均,$V_t = \beta_2 V_{t-1} + (1-\beta_2)g_t^2$
- 避免了二阶动量持续累积、导致训练过程提前结束
Adam
- 集大成者:把一阶动量和二阶动量都用起来,Adaptive Momentum
- SGD-M在SGD基础上增加了一阶动量
- AdaGrad和AdaDelta在SGD基础上增加了二阶动量
- 一阶动量滑动平均:$m_t = \beta_1 m_{t-1} + (1-\beta_1) g_t$
- 二阶动量滑动平均:$V_t = \beta_2 V_{t-1} + (1-\beta_2)g_t^2$
- 集大成者:把一阶动量和二阶动量都用起来,Adaptive Momentum
Nadam
- look ahead Adam
- 把Nesterov的one step try加上:$g_t = \nabla f(w_t-\alpha m_{t-1}/\sqrt {V_{t-1}})$
- 再Adam更新两个动量
经验超参
- $momentum=0.9$
- $\beta_1=0.9$
- $\beta_2=0.999$
- $m_0 = 0$
- $V_0 = 0$
- 上面的图上可以看出,初期的$m_t$和$V_t$会无限接近于0,此时可以进行误差修正:$factor=\frac{1}{1-\beta^t}$
AdamW
- 在adaptive methods中,解耦weight-decay和loss-based gradient在ERM过程中的绑定downscale的关系
- 实质就是将导数项后移
