nms | Less is More

Non-maximum suppression：非极大值抑制算法，本质是搜索局部极大值，抑制非极大值元素

[nms]：standard nms，当目标比较密集、存在遮挡时，漏检率高

[soft nms]：改变nms的hard threshold，用较低的分数替代0，提升recall

[softer nms]：引入box position confidence，通过后处理提高定位精度

[DIoU nms]：采用DIoU的计算方式替换IoU，因为DIoU的计算考虑到了两框中心点位置的信息，效果更优

[fast nms]：YOLOACT引入矩阵三角化，会比Traditional NMS抑制更多的框，性能略微下降

[cluster nms]：CIoU提出，弥补Fast NMS的性能下降，运算效率比Fast NMS下降了一些

[mask nms]：mask iou计算有不可忽略的延迟，因此比box nms更耗时

[matrix nms]：SOLO将mask IoU并行化，比FAST-NMS还快，思路和FAST-NMS一样从上三角IoU矩阵出发，可能造成过多抑制。

[WBF]：加权框融合，Kaggle胸片异物比赛claim有用，速度慢，大概比标准NMS慢3倍，WBF实验中是在已经完成NMS的模型上进行的

nms
- 过滤+迭代+遍历+消除
  - 首先过滤掉大量置信度较低的框，大于confidence thresh的box保留
  - 将所有框的得分排序，选中最高分的框
  - 遍历其余的框，如果和当前最高分框的IOU大于一定阈值(nms thresh)，就将框删除(score=0)
  - 从未处理的框中继续选一个得分最高的，重复上述过程
- when evaluation
  - iou thresh：留下的box里面，与gt box的iou大于iou thresh的box作为正例，用于计算出AP和mAP，通过调整confidence thresh可以画出PR曲线

softnms
- 基本流程还是nms的贪婪思路，过滤+迭代+遍历+衰减
- re-score function：high overlap decays more
  - linear：
    - for each $iou(M,b_i)>th$， $s_i=s_i(1-iou)$
    - not continuous，sudden penalty
  - gaussian：
    - for all remaining detection boxes，$s_i=s_i e^{-\frac{iou(M,b_i)}{\sigma}}$
- 算法流程上未做优化，是针对精度的优化

softer nms
- 跟soft nms没关系
- 具有高分类置信度的边框其位置并不是最精准的
- 新增加了一个定位置信度的预测，使其服从高斯分布
- infer阶段边框的标准差可以被看做边框的位置置信度，与分类置信度做加权平均，作为total score
- 算法流程上未做优化，完全是精度的优化

DIoU nms
- 也是为了解决hard nms在密集场景中漏检率高的问题
- 但是不同于soft nms的是，D的改进在iou计算上，而不是在score
- diou的计算：$diou = iou-\frac{\rho^2(b_1, b_2)}{c^2}$
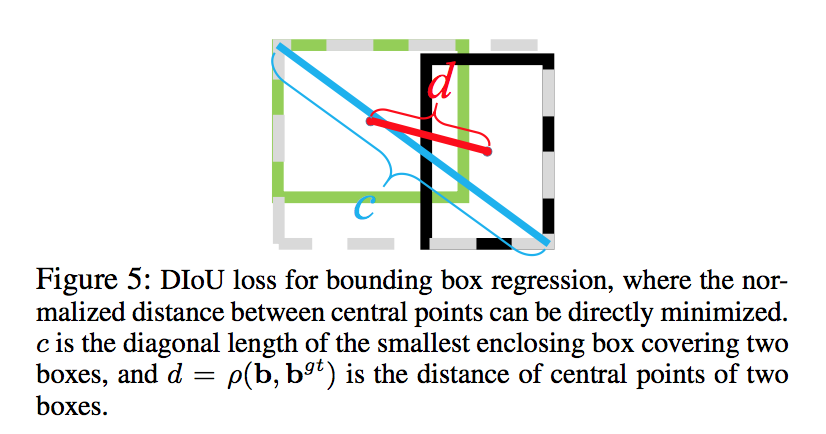
- 算法流程上未做优化，仍旧是精度的优化

fast nms
- yoloact提出
- 主要效率提升在于用矩阵操作替换遍历，所有框同时被filter掉，而非依次遍历删除
- iou上三角矩阵
  - iou上三角矩阵的每一个元素都是行号小于列号
  - iou上三角矩阵的每一个行，对应一个bnd box，与其他所有score小于它的bnd box的iou
  - iou上三角矩阵的每一个列，对应一个bnd box，与其他所有score大于它的bnd box的iou
  - fast nms在iou矩阵每一列上求最大值，如果这个最大值大于iou thresh，说明当前列对应的bnd box，存在一个score大于它，且和它重叠度较高的bnd box，因此要把这个box过滤掉
- 有精度损失
  - 场景：
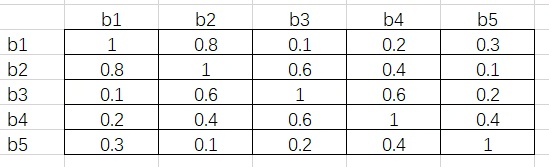
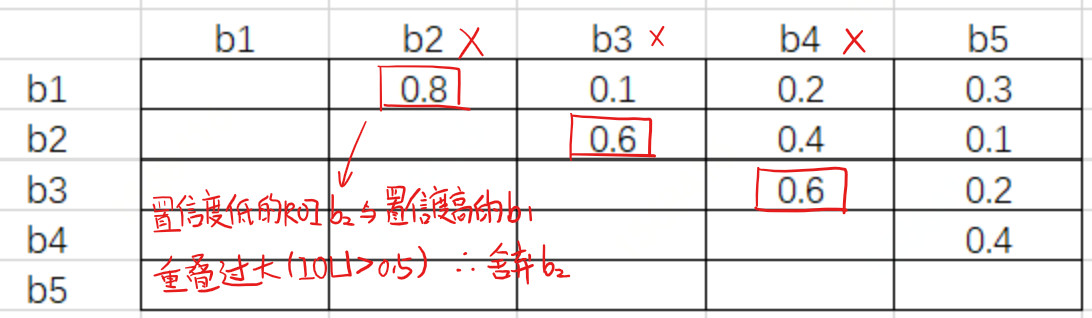
  - 如果是hard nms的话，首先遍历b1的其他box，b2就被删除了，这是b3就不存在高重叠框了，b3就会被留下，但是在fast nms场景下，所有框被同时删除，因此b2、b3都没了。

cluster nms
- 针对fast nms性能下降的弥补
- fast nms性能下降，主要问题在于过度抑制，并行操作无法及时消除high score框抹掉对后续low score框判断的影响
- 算法流程上，将fast nms的一次阈值操作，转换成少数几次的迭代操作，每次都是一个fast nms
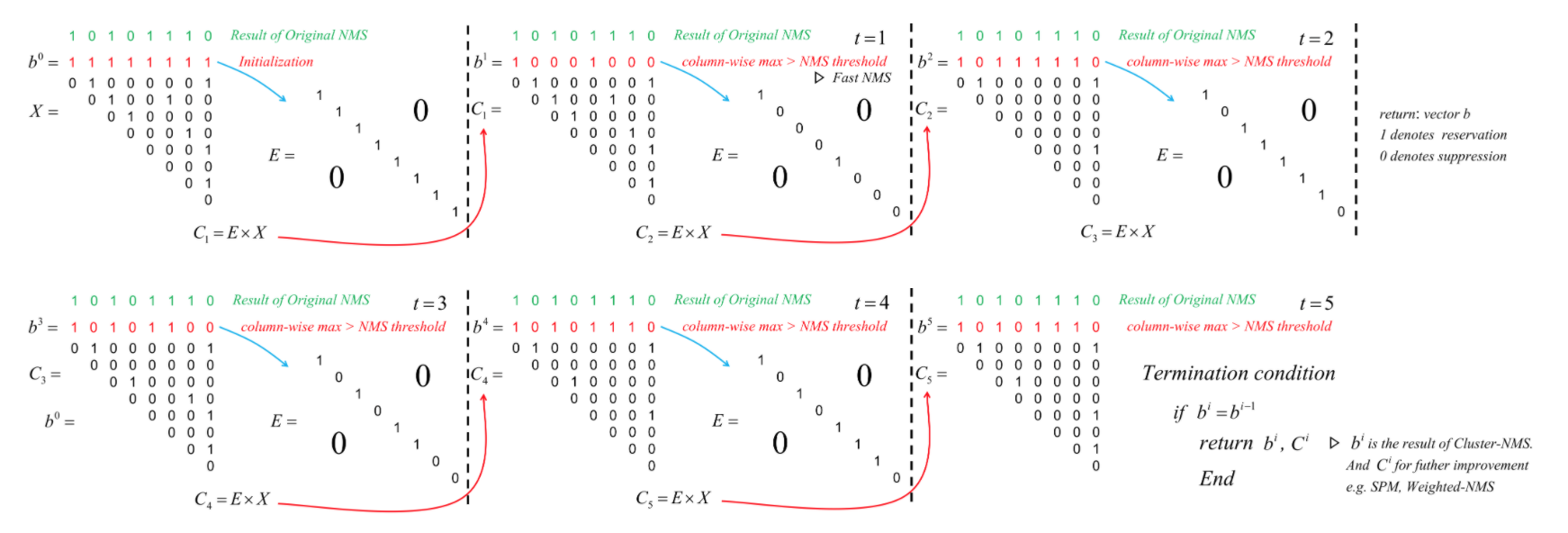
  - 图中X表示iou矩阵，b表示nms阈值二值化以后的向量，也就是fast nms里面那个保留／抑制向量
  - 每次迭代，算法将b展开成一个对角矩阵，然后左乘iou矩阵
  - 直到出现某两次迭代后， b保持不变了，那么这就是最终的b
- cluster nms的迭代操作，其实就是在省略上一次Fast NMS迭代中被抑制的框对其他框的影响
- 数学归纳法证明，cluster nms的结果与hard nms完全一致，运算效率比fast nms下降了一些，但是比hard nms快得多
- cluster nms的运算效率不与cluster数量有关，只与需要迭代次数最多的那一个cluster有关

mask nms
- 从检测框形状的角度拓展出来，包括但不限于mask nms、polygon nms以及inclined nms
- iou的计算方式有一种是mmi：$mmi=max(\frac{I}{I_A}, \frac{I}{I_B})$

matrix nms
- 学习soft nms：decay factor
- one step further：迭代改并行
- 对于某个object $m_j$的score进行penalty的时候考虑两部分影响
  - 迭代某个$m_i$时，对后续lower score的$m_j$的影响
  - 一是正面影响$f(iou_{i,j})\ linear/guassian$：这个框保留，那么后续框都要基于与其的iou做decay
  - 二是反向影响$f(iou_{*,i})=max_{\forall s_k>s_i}f(iou_{k,i})$：如果这个框不保留，那么对于后续框来讲，应该消除这个框对其的decay，选最大值的意义是当前mask被抑制最有可能就是和他重叠度最大的那个mask干的（因为对应的正面影响1-iou最小）

final decay factor：$decay_j=min_{\forall s_i > s_j}\frac{f(iou_{i,j})}{f(iou_{*,i})}$

算法流程

  <img src="nms/matrixnms.png" width="50%;" />

* 按照原论文的实现，decay永远大于等于1，因为每一列的iou_cmax永远大于等于iou，从论文的思路来看，每个mask的decay是它之前所有mask的影响叠加在一起，所以应该是乘积而不是min：

    1
2
3
4
5
6
7
8
9
10
11
12
# 原论文实现
if method=='gaussian':
    decay = np.exp(-(np.square(iou)-np.square(iou_cmax))/sigma)
else:
    decay = (1-iou)/(1-iou_cmax)
decay = np.min(decay, axis=0)

# 改进实现
if method=='gaussian':
    decay = np.exp(-(np.sum(np.square(iou),axis=0)-np.square(iou_cmax))/sigma)
else:
    decay = np.prod(1-iou)/(1-iou_cmax)