参考:https://gombru.github.io/2019/04/03/ranking_loss/,博主实验下来觉得Triplet Loss outperforms Cross-Entropy Loss
综述
metric learning
- 常规的cls loss系列(CE、BCE、MSE)的目标是predict a label
- metric loss系列的目标则是predict relative distances between inputs
- 常用场景:人脸 & fine-grained
relation between samples
- first get the embedded representation
- then compute the similarity score
- binary (similar / dissimilar)
- regression (euclidian distance)
大类:不管叫啥,主体上就两类,二元组和三元组
common target:拉近类内距离,拉大类间距离
pairs
- anchor + sample
- positive pairs:distance —> 0
- negative pairs:disctance > a margin
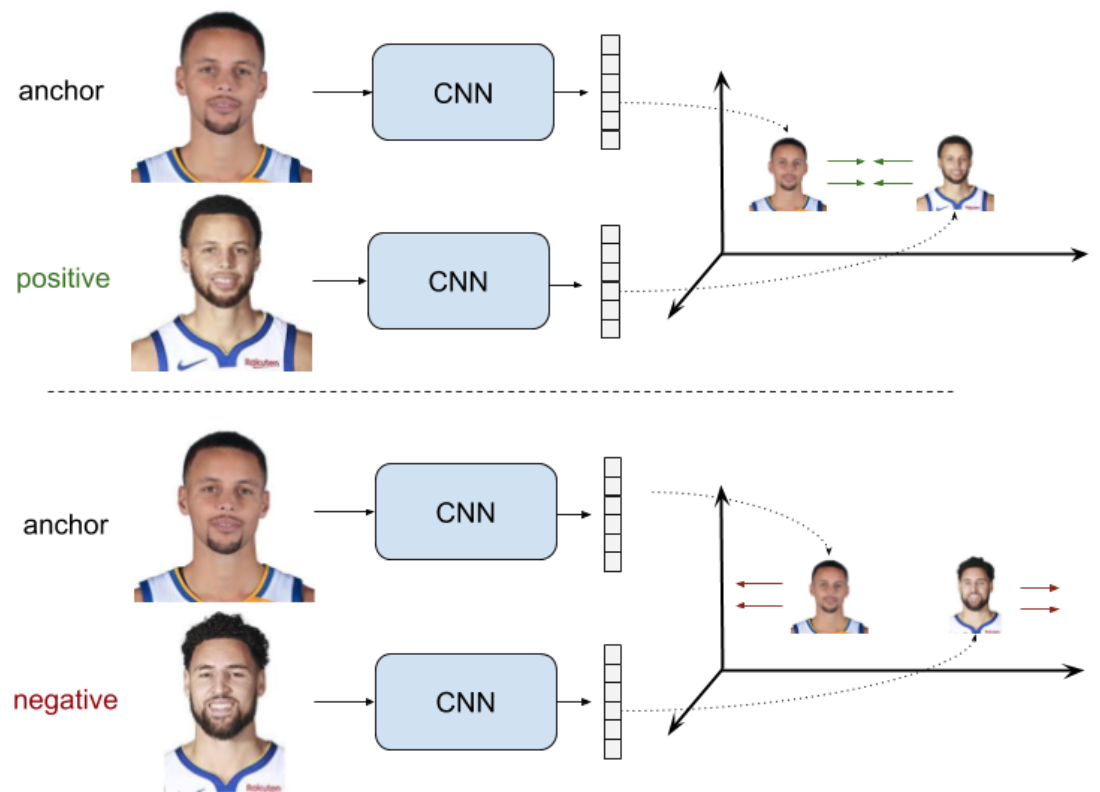
- anchor + sample
- triplets
- anchor + pos sample + neg sample
- target:(dissimilar distance - similar distance) —> a margin
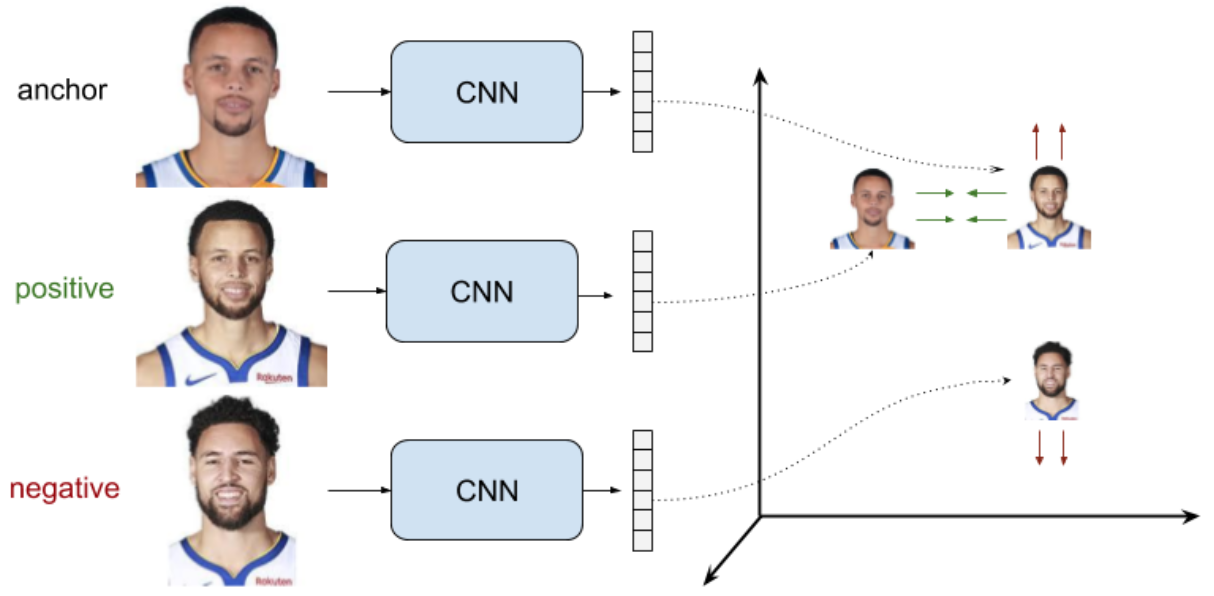
papers
[siamese network] Signature Verification using a ‘Siamese’ Time Delay Neural Network:1993,lecun,孪生网络始祖,俩个子网络sharing weights,距离用的是cosine distance,loss直接优化距离,优化target是个定值cosine=1.0/-1.0
[contrastive loss] Dimensionality Reduction by Learning an Invariant Mapping:2006,lecun,contrastive loss始祖,研究的是高维特征向量向低维映射的非线性层,距离用的是euclidean distance,loss优化的是squared distance,优化target是0和m,similar pairs仍旧会被推向一个定点,没有解决论文声称的uniform distribution
[triplet-loss] Learning Fine-grained Image Similarity with Deep Ranking:2014,Google,用了三元组,提出了triplet-loss
[facenet] FaceNet: A Unified Embedding for Face Recognition and Clustering:2015,Google,用来识别人脸,用了三元组和triplet-loss,squared euclidean distance,优化目标是同类和异类pair之间的相对距离,困难样本(semi-hard & hard)对收敛起作用(加速/local minima),triplet-loss考虑了类间的离散性,但没有考虑类内的紧凑性
[center-loss] A Discriminative Feature Learning Approach for Deep Face Recognition:2016,也是用在人脸任务上,优化目标是类内的绝对距离,而不是建模相对关系,center-loss直接优化的是类间的间凑性,类间的离散性靠的是softmax loss
[triplet-center-loss] Triplet-Center Loss for Multi-View 3D Object Retrieval:2018,东拼西凑水论文
[Hinge-loss] SVM margin
[circle-loss] Circle Loss: A Unified Perspective of Pair Similarity Optimization:2020CVPR,旷视,提出了cls loss和metric loss的统一形式$minimize(s_n - s_p+m)$,在此基础上提出circle loss作为优化目标$(\alpha_n s_n - \alpha_p s_p) = m$,在toy scenario下展示了分类边界和梯度的改善。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
[Hierarchical Similarity] Learning Hierarchical Similarity Metrics:2012CVPR,
[Hierarchical Triplet Loss] Deep Metric Learning with Hierarchical Triplet Loss:2018ECCV,
- Hierarchical classicification应该单独做一个系列,tobeadded
一些待明确的问题
- anchor怎么选:facenet中说明,每个mini-batch中每个类别必须都有
- pairs怎么实现(困难的定义):facenet中说明,hard distance sample in mini-batch
- hingeloss & SVM推导
- 常规使用?结合cls loss和metric loss还是只用metric loss:cls loss和metric loss本质上是一样的,都是希望同类样本输出一样,不同类样本输出不一样,只不过前者具有概率意义,后者具有距离意义。上面列出来的只有center loss是要跟cls loss结合起来用的,因为他只针对类内,不足以推动整个模型。
Signature Verification using a ‘Siamese’ Time Delay Neural Network
- 动机
- verification of written signatures
- propose Siamese
- two identical sub-networks
- joined at their outputs
- measure the distance
- verification process
- a stored feature vector
- a chosen threshold
- 方法
- network
- two inputs:extracting features
- two sub-networks:share the same weights
- one output:cosine of the angle between two feature vectors
- target
- two real signatures:cosine=1.0
- with one forgery:cosine=-0.9 and cosine=-1.0
- dataset
- 50% genuine:genuine pairs
- 40% genuine:forgery pairs
- 10% genuine:zero-effort pairs
- network
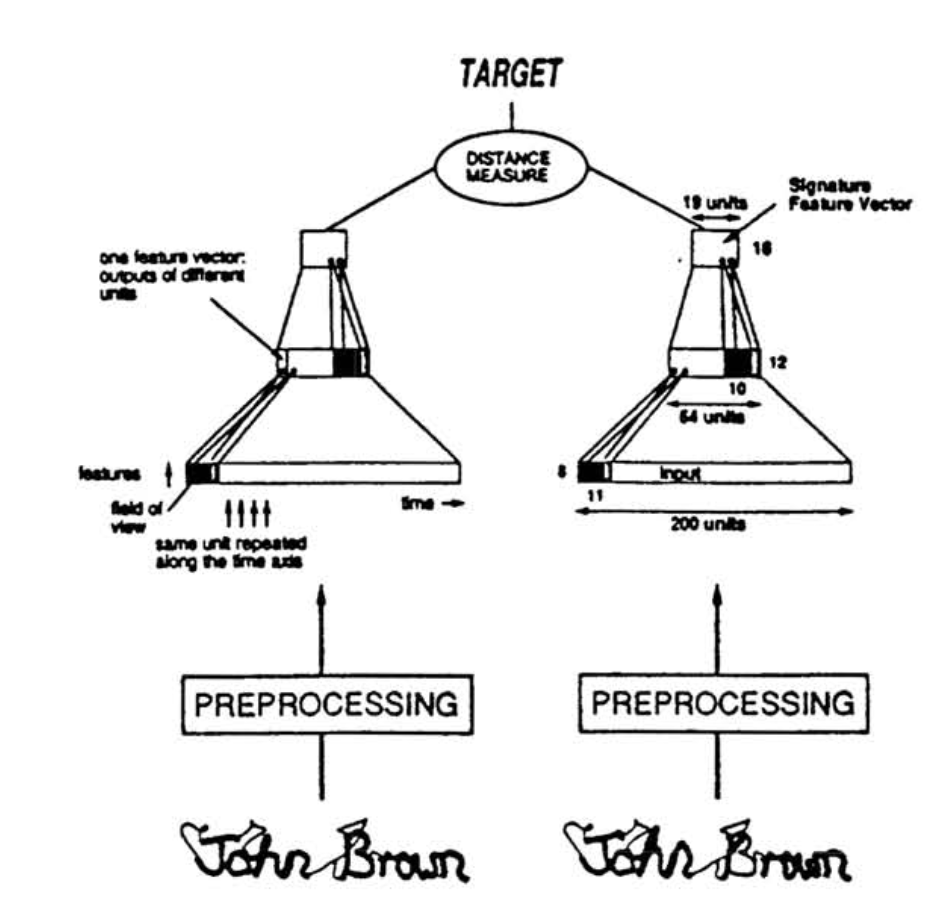
Dimensionality Reduction by Learning an Invariant Mapping
动机
- dimensionality reduction
- propose Dimensionality Reduction by Learning an Invariant Mapping (DrLIM)
- globally co- herent non-linear function
- relies solely on neighbor- hood relationships
- invariant to certain transformations of the inputs
论点
- most existing dimensionality reduction techniques
- they do not produce a function (or a mapping) from input to manifold
- new points with unknown relationships with training samples cannot be processed
- they tend to cluster points in output space
- a uniform distribution in the outer manifolds is desirable
- proposed DrLIM
- globally coherent non-linear function
- neighborhood relationships that are independent from any distance metric
- invariant to complicated non-linear trnasformations
- lighting changes
- geometric distortions
- can be used to map new samples
- empoly contrastive loss
- neighbors are pulled together
- non-neighbors are pushed apart
- energy based model
- euclidean distance
- approximates the “semantic similarity”of the inputs in input space
- most existing dimensionality reduction techniques
方法
contrastive loss
conventional loss sum over samples
contrastive loss sum over pairs $(X_1, X_2, Y)$
- similar pairs:$Y=0$
- dissimilar:$Y=1$
euclidean distance
$L = (1-Y)\sum L_s ||G_w(X_1)-G_w(X_2)||_2 + Y\sum L_d ||G_w(X_1)-G_w(X_2)||_2$
$L_s$ should results in low values for similar pairs
- $L_d$ should results in high values for dissimilar pairs
- exact form:$L(W,Y,X_1,X_2) = (1-Y)\frac{1}{2}(D^2) + (Y)\frac{1}{2} \{max(0,m-D)\}^2$
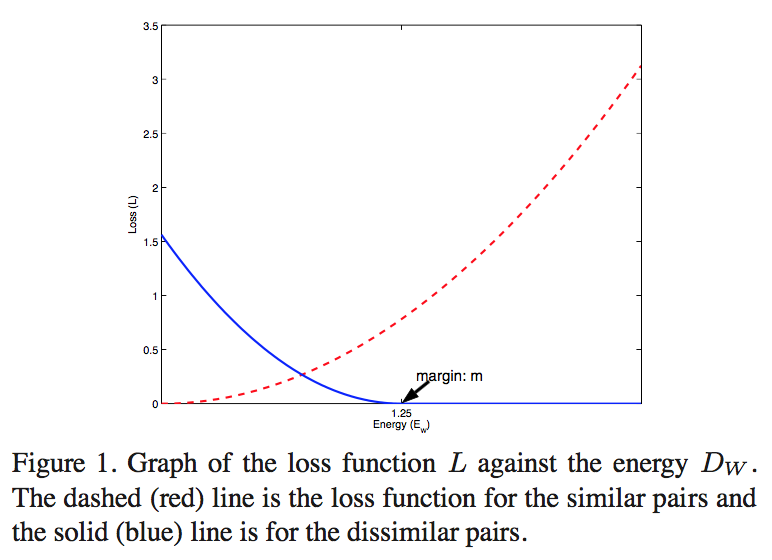
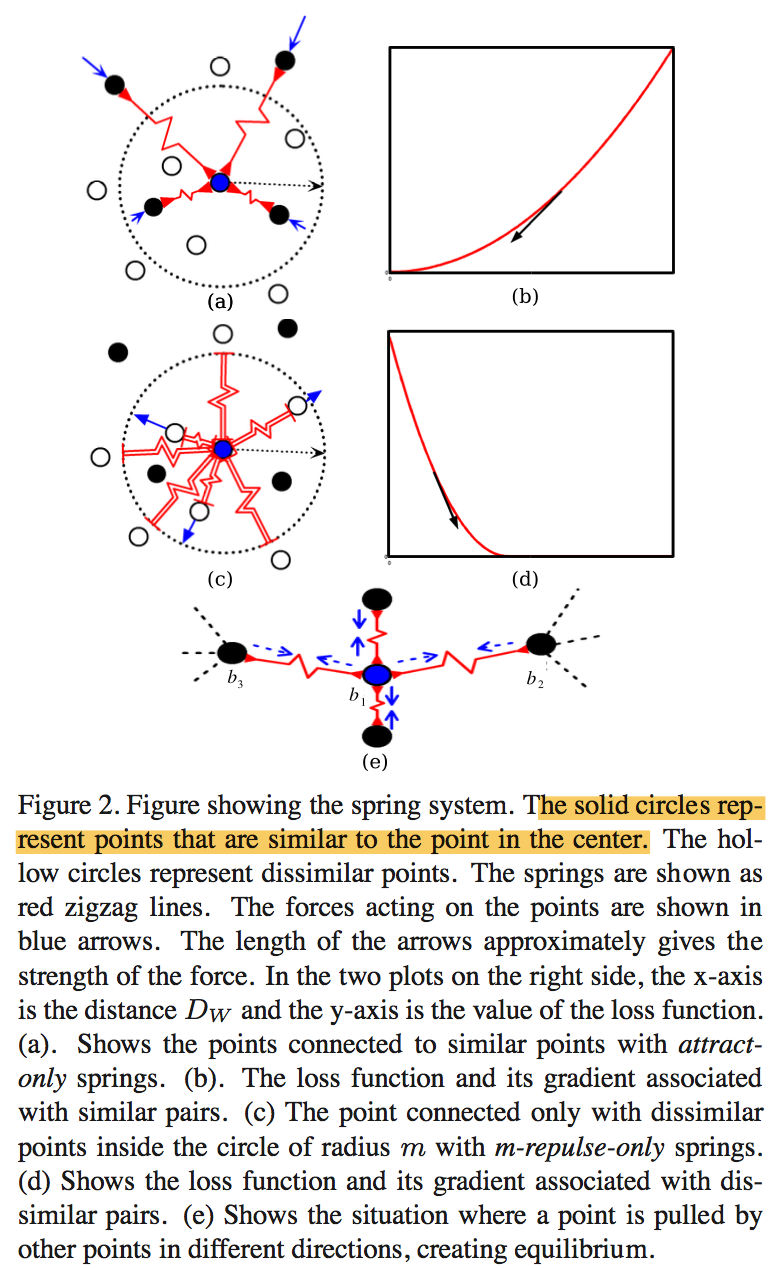
spring model analogy
- similar partial loss相当于给弹簧施加了一个恒定的力,向中心点挤压
dissimilar partial loss只对圈内的点施力,推出圈外就不管了
FaceNet: A Unified Embedding for Face Recognition and Clustering
动机
face tasks
- face verification: is this the same person
- face recognition: who is the person
- clustering: find common people among the faces
learn a mapping
- compact Euclidean space
where the Euclidean distance directly correspond to face similarity

论点
traditionally training classification layer
generalizes well to new faces? indirectness
large dimension feature representation inefficiency
use siamese pairs
- the loss encourages all faces of one identity to project onto a single point
this paper
- employ triplet loss
- target:separate the positive pair from the negative by a distance margin
- allows the faces of one identity to live on a manifold
- obtain face embedding
- l2 norm
- a fixed d-dims hypersphere
- large dataset
- to attain the appropriate invariances to pose, illumination, and other variational conditions
architecture
- explore two different deep network
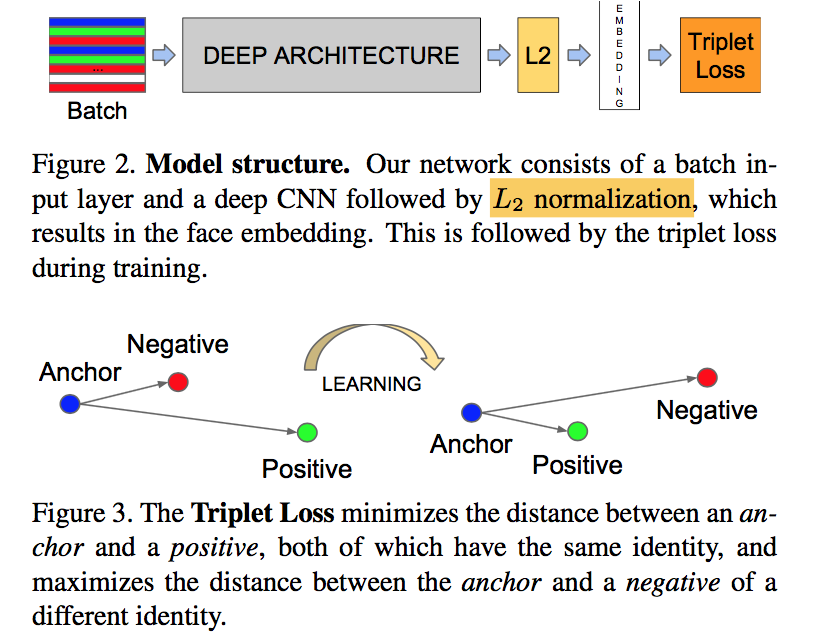
- employ triplet loss
方法
input:三元组,consist of two matching face thumbnails and a non-matching one
ouput:特征描述,a compact 128-D embedding living on the fixed hypersphere $||f(x)||_2=1$
triple-loss
- target:all anchor-pos distances are smaller than any anchor-neg distances with a least margin $\alpha$
- $L = \sum_i^N [||f(x_i^a) - f(x_i^p)||_2^2 - ||f(x_i^a) - f(x_i^n)||_2^2 + \alpha]$
- hard triplets
hard samples
- $argmax_{x_i^p}||f(x_i^a) - f(x_i^p)||_2^2$
- $argmin_{x_i^n}||f(x_i^a) - f(x_i^n)||_2^2$
- infeasible to compute over the whole set:mislabelled and poorly imaged faces would dominate the hard positives and negatives
- off-line:use recent checkpoint to compute on a subset
- online:select in mini-batch
mini-batch:
- 每个类别都必须有正样本
- 负样本是randomly sampled
hard sample
- use all anchor-positive pairs
- selecting the hard negatives
- hardest negatives can lead to bad local minima in early stage
- 先pick semi-hard:$||f(x_i^a) - f(x_i^p)||_2^2 < ||f(x_i^a) - f(x_i^n)||_2^2$
network
- 一种straight的网络,引入了1x1 conv先压缩通道
- Inception models:20x fewer params,5x fewer FLOPS
metric
- same/different是由a squared L2 distance决定
- 因此测试结果是d的函数
- 定义true accepts:圈内对的,$TA(d)=\{(i,j)\in P_{same}, with D(x_i,x_j)\leq d\}$
定义false accepts:圈内错的,$FA(d)=\{(i,j)\in P_{diff}, with D(x_i,x_j)\leq d\}$
定义validation rate:$VAL(d) = \frac{|TA(d)|}{|P_{same}|}$
- 定义false accept rate:$FAR(d) = \frac{|FA(d)|}{|P_{diff}|}$
A Discriminative Feature Learning Approach for Deep Face Recognition
动机
- enhance the discriminationative power of the deeply learned features
- joint supervision
- softmax loss
- center loss
- two key learning objectives
- inter-class dispension
- intra-class compactness
论点
- face recognition task requirement
- the learned features need to be not only separable but also discriminative
- generalized enough for the new unseen samples
- the softmax loss only encourage the separability of features
- 对分类边界、类内类间分布没有直接约束
- contrastive loss & triplet loss
- training pairs or triplets dramatically grows
- slow convergence and instability
- we propose
- learn a center
- simultaneously update the center and optimize the distances
- joint supervision
- softmax loss forces the deep features of different classes staying apart
- center loss efficiently pulls the deep features of the same class to their centers
- to be more discriminationative
- the inter-class features differences are enlarged
- the intra-class features variations are reduced
- face recognition task requirement
方法
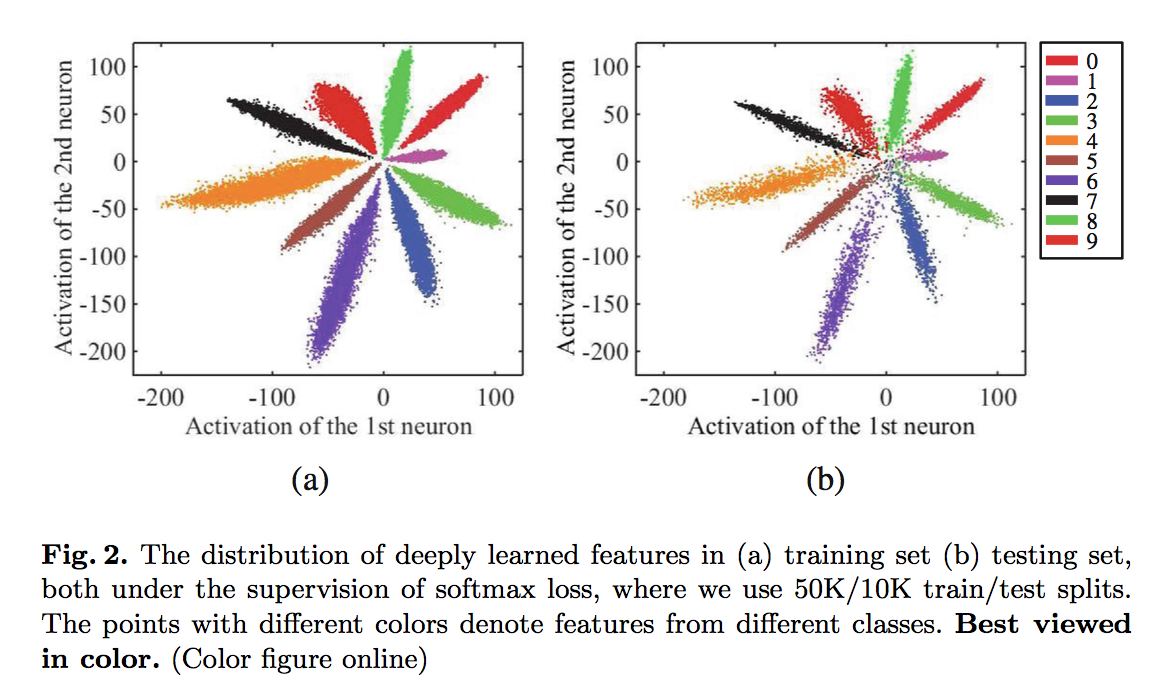
softmax vis
- 最后一层hidden layer使用两个神经元
- so that we can directly plot
separable but still show significant intra-class variations
center loss
$L_c = \frac{1}{2} \sum_1^m ||x_i - c_{y_i}||_2^2$
update class center on mini-batch:
joint supervision:
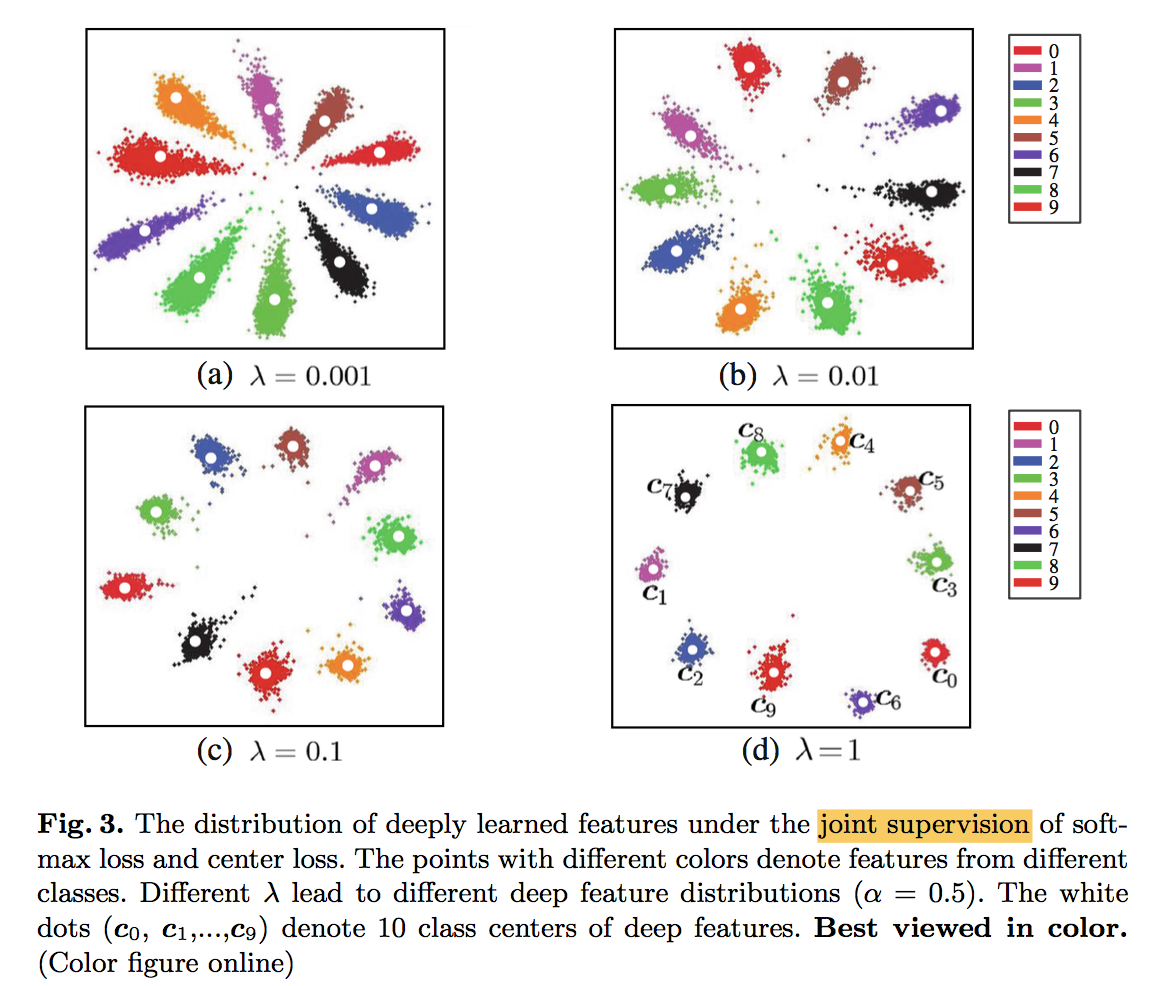
discussion
- necessity of joint supervision
- solely softmax loss —-> large intra-class variations
- solely center loss —-> features and centers will degraded to zeros
- compared to contrastive loss and triplet loss
- using pairs:suffer from dramatic data expansion
- hard mining:complex recombination
- optimizing target:
- center loss直接针对intra-class compactness,类内用距离来约束,类间用softmax来约束
- contrastive loss也是直接优化绝对距离,类内&类间都用距离来约束
- triplet loss是建模相对关系,类内&类间都用距离来约束
- necessity of joint supervision
architecture
- local convolution layer:当数据集在不同的区域有不同的特征分布时,适合用local-Conv,典型的例子就是人脸识别,一般人的面部都集中在图像的中央,因此我们希望当conv窗口滑过这块区域的时候,权重和其他边缘区域是不同的
参数量暴增:kernel_size kernel_size output_size output_size input_channel * output_channel
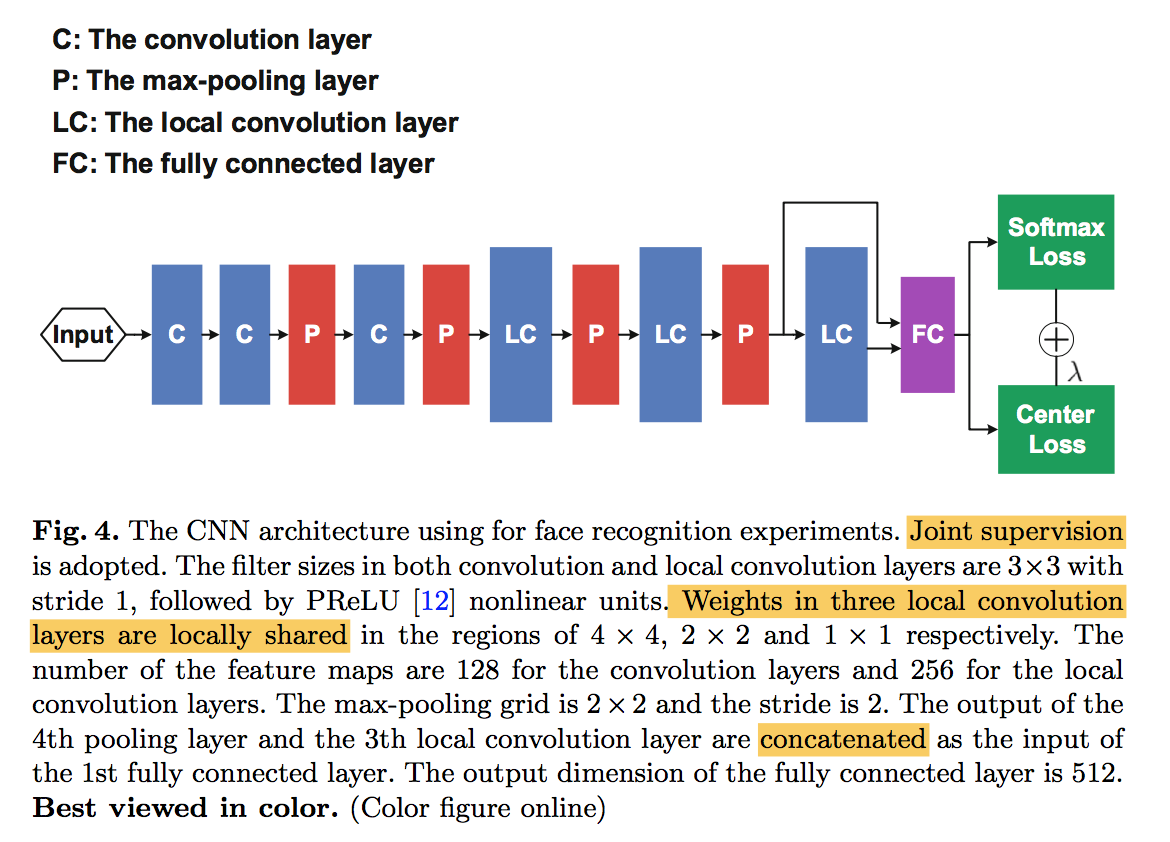
实验
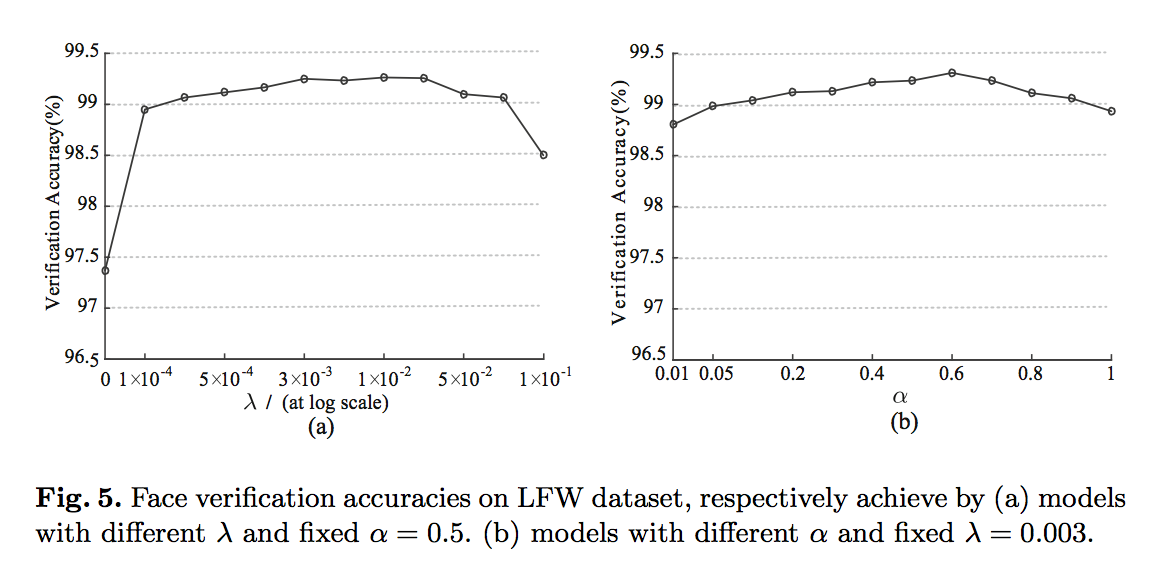
hyperparam:$\lambda$ and $\alpha$
- fix $\alpha=0.5$ and vary $\lambda$ from 0-0.1
- fix $\lambda=0.003$ and vary $\alpha$ from 0.01-1
结论是remains stable across a large range,没有给出最佳/建议
我的实验
- 加比不加训练慢得多
- 在Mnist上测试同样的epoch加比不加准确率低
- 之所以Center Loss是针对人脸识别的Loss是有原因的,个人认为人脸的中心性更强一些,也就是说一个人的所有脸取平均值之后的人脸我们还是可以辨识是不是这个人,所以Center Loss才能发挥作用
Circle Loss: A Unified Perspective of Pair Similarity Optimization
动机
- pair similarity
- circular decision boundary
- unify cls-based & metric-based data
- class-level labels
- pair-wise labels
论点
there is no intrinsic difference between softmax loss & metric loss
- minimize between-class similarity $s_n$
- maximize within- class similarity $s_p$
- reduce $s_n - s_p$
short-commings
- lack of flexibility:$s_p$和$s_n$的优化速度可能不同,一个快收敛了一个还很差,这时候用同样的梯度去更新就非常inefficient and irrational,就左图来说,下面的点相对上面的点,$s_n$更小(更接近op),$s_p$更小(更远离op),vice versa,但是决策平面对三个点相对于$s_n$和$s_p$的梯度都是一样的(1和-1)。
ambiguous convergence status:用一个hard distance margin来描述decision boundary还不够discriminative,hard decision boundary上各点其实还是有差别的,假设存在一个optimum($s_p=1 \ \& \ s_n=0$),那么左图决策平面上两个点,相对optimum的意义明显不一样,决策平面应该是个围绕optimum的圆圈。
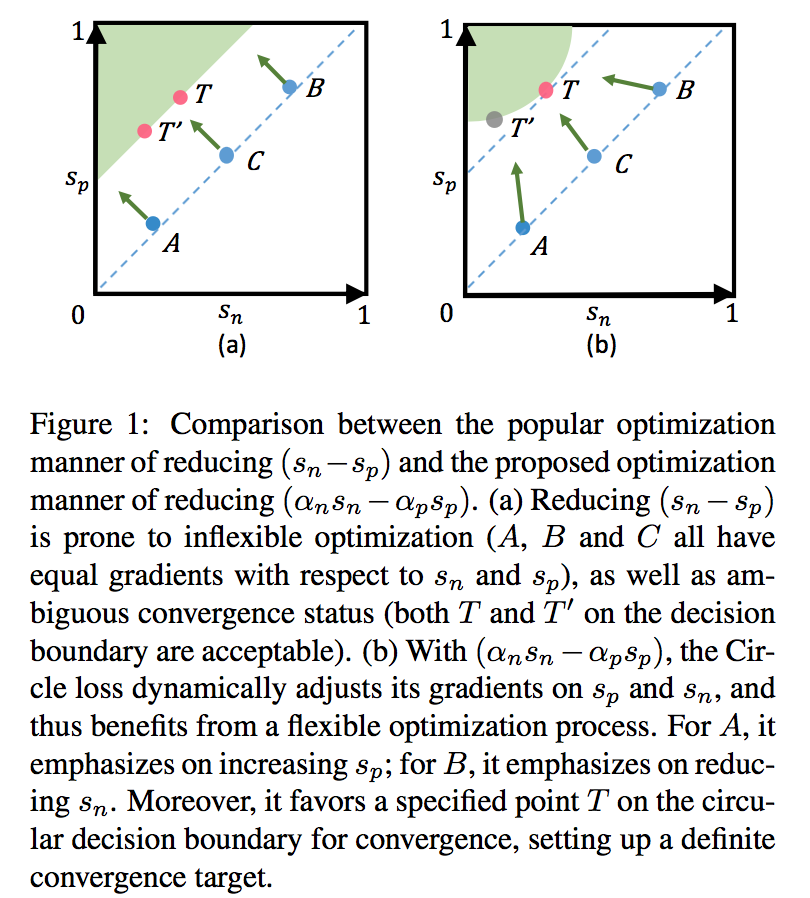
propose circle loss
- independent weighting factors:离optimum越远的penalty strength越大,这一项直接以距离为优化目标的loss都是满足的
- different penalty strength:$s_p$和$s_n$ learn at different paces,类内加权,加权系数是learnable params
- $(\alpha_n s_n - \alpha_p s_p) = m$:yielding a circle shape
方法
核心:$(\alpha_n s_n - \alpha_p s_p) = m$
self-paced weighting
given optimum $O_p$ and $O_n$,for each similarity score:
cut-off at zero
对于远离optimum的点梯度放大,接近optimum的点(快收敛)梯度缩小
softmax里面通常不会对同类样本间做这种rescaling的,因为它希望所有样本value都达到贼大
Circle loss abandons the interpretation of classifying a sample to its target class with a large probability
margin
- adding a margin m reinforces the optimization
- take toy scenario
- 最终整理成:$(s_n-0)^2 + (s_p-1)^2 = 2m^2$
- op target:$s_p > 1-m$,$s_n < m$
- relaxation factor $m$:controls the radius of the decision boundary
unified perspective
- tranverse all the similarity pairs:$\{s_p^i\}^K$和$\{s_n^j\}^N$
- to reduce $(s_n^j - s_p^i)$:$L_{uni}=log[1+\sum^K_i \sum^N_j exp(\lambda (s_n^j - s_p^i + m))]$
- 解耦(不会同时是$s_p$和$s_n$):$L_{uni}=log[1+\sum^N_j exp(\lambda (s_n^j + m))\sum^K_i exp(\lambda (-s_p^i))]$
- given class labels:
- we get $(N-1)$ between-class similarity scores and $(1)$ within-class similarity score
- 分母翻上去:$L = -log \frac{exp(\lambda (s_p-m))}{exp(\lambda (s_p-m)) + \sum^{N-1}_j exp(\lambda (s_n^j))}$
- 就是softmax
- given pair-wise labels:
- triplet loss with hard mining:find pairs with large $s_n$ and low $s_p$
- use infinite:$L=lim_{\lambda \to \inf} \frac{1}{\lambda} L_{uni}$
实验
- Face recognition
- noisy and long-tailed data:去噪并且去掉稀疏样本
- resnet & 512-d feature embeddings & cosine distance
- $\lambda=256$,$m=0.25$
- Person re-identification
- $\lambda=128$,$m=0.25$
- Fine-grained image retrieval
- 车集和鸟集
- bn-inception & 512-d embeddings
- P-K sampling
- $\lambda=80$,$m=0.4$
- hyper-params
- the scale factor $\lambda$:
- determines the largest scale of each similarity score
- Circle loss exhibits high robustness on $\lambda$
- the other two becomes unstable with larger $\lambda$
- owing to the decay factor
- the relaxation factor m:
- determines the radius of the circular decision boundary
- surpasses the best performance of the other two in full range
- robustness
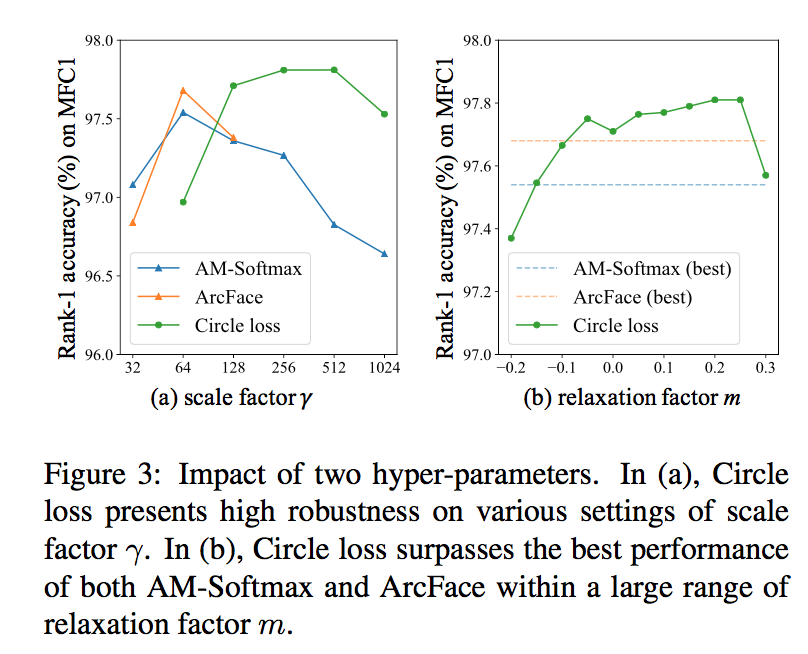
- the scale factor $\lambda$:
- Face recognition
inference
- 对人脸类任务,通常用训练好的模型生成一个人脸标准底库,然后每次推理的时候得到测试数据的特征向量,并在标准底库中搜索相似度最高的特征,完成人脸识别过程。