17年的paper,引用量15,提出了网路结构,但是没分析为啥有效,垃圾
Bilinear CNNs for Fine-grained Visual Recognition
动机
- fine-grained classification
- propose a pooled outer product of features derived from two CNNs
- 2 CNNs
- a bilinear layer
- a pooling layer
- outperform existing models and fairly efficient
- effective at other image classification tasks such as material, texture, and scene recognition
论点
- fine-grained classification tasks require
- recognition of highly localized attributes of objects
- while being invariant to their pose and location in the image
- previous techniques
- part-based models
- construct representations by localizing parts
- more accurate but requires part annotations
- holistic models
- construct a representation of the entire image
- texture descriptors:FV,SIFT
- STN:augment CNNs with parameterized image transformations
- attention:use segmentation as a weakly-supervised manner
- part-based models
- Our key insight is that several widely-used texture representations can be written as a pooled outer product of two suitably designed features
- several widely-used texture representations
- two suitably designed features
- the bilinear features are highly redundant
- dimensionality reduction
- trade-off between accuracy
We also found that feature normalization and domain-specific fine-tuning offers additional benefits
combination
- concatenate:additional parameters to fuse
- an outer product:no parameters
- sum product:can achieve similar approximations
- “two-stream” architectures
- one used to model two- factor variations such as “style” and “content” for images
- in our case is to model two factor variations in location and appearance of parts:但并不是explicit modeling因为最终是个分类头
- one used to analyze videos modeling the temporal aspect and the spatial aspect
- dimension reduction
- two 512-dim feature results in 512x512-dim
- earlier work projects one feature to a lower-dimensional space, e.g. 64-dim—>512x64-dim
- we use compact bilinear pooling to generate low-dimensional embeddings (8-32x)
- fine-grained classification tasks require
方法
architecture
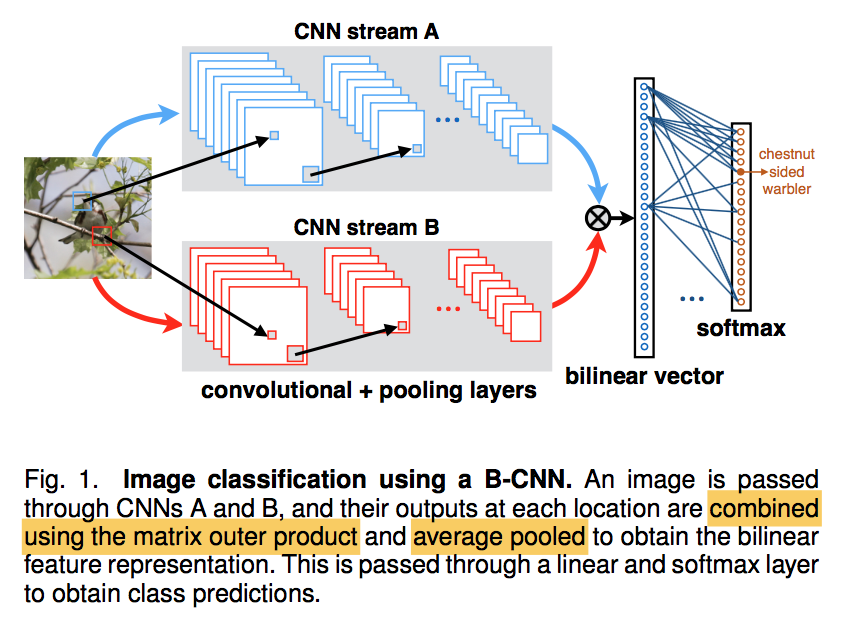
- input $(l,I)$:takes an image and a location,location generally contains position and scale
- quadruple $B=(f_A, f_B, P, C)$
- A、B两个CNN:conv+pooling layers,
- P:pooling function
- combined A&B outputs using the matrix outer product
- average pooling
- C:logistic regression or linear SVM
- we found that linear models are effective on top of bilinear features
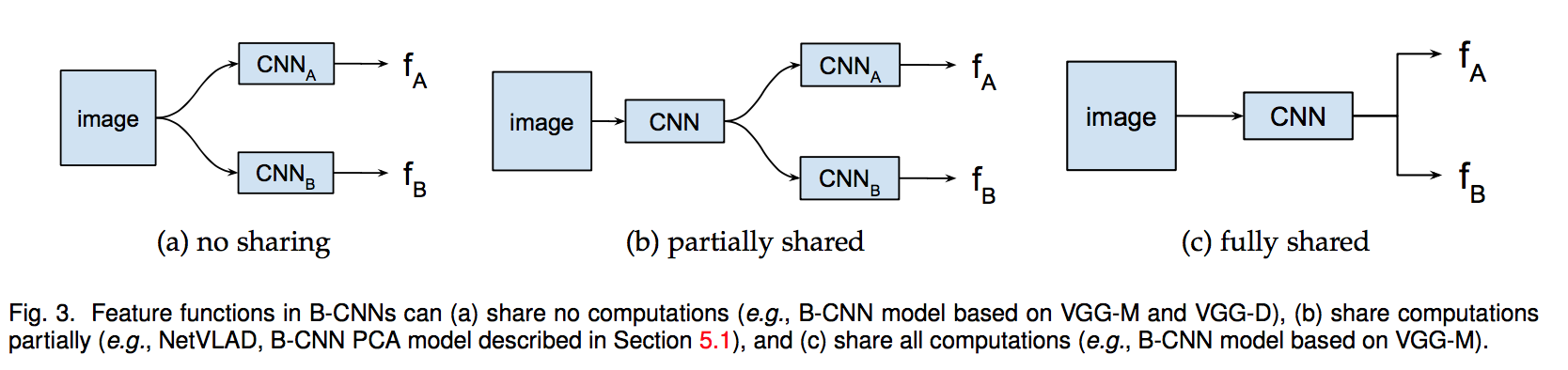
CNN
independent/partial shared/fully shared
bilinear combination
for each location
$bilinear(l,I,f_A,f_B)=f_A(l,I)^T f_B(l,I)$
pooling function combines bilinear features across all locations
$\Phi (I) = \sum_{l\in L} bilinear(l,I,f_A,f_B)$
same feature dimension K for A & B,e.g. KxM & KxN respectively,$\Phi(I)$ is size MxN
Normalization
- a signed square root:$y=sign(x)\sqrt {|x|}$
follow a l2 norm:$z = \frac{y}{||y||_2}$
improves performance in practice
classification
- logistic regression or linear SVM
- we found that linear models are effective on top of bilinear features
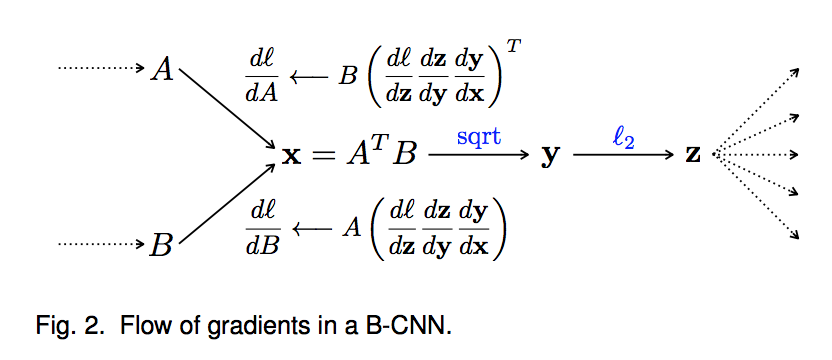
back propagation
$\frac{dl}{dA}=B(\frac{dl}{dx})^T$,$\frac{dl}{dB}=A(\frac{dl}{dx})^T$
Relation to classical texture representations:放在这一节撑篇幅??
- texture representations can be defined by the choice of the local features, the encoding function, the pooling function, and the normalization function
- choice of local features:orderless aggregation with sum/max operation
- encoding function:A non-linear encoding is typically applied to the local feature before aggregation
- normalization:normalization of the aggregated feature is done to increase invariance
- end-to-end trainable
- texture representations can be defined by the choice of the local features, the encoding function, the pooling function, and the normalization function