regression loss

1. 损失函数用来评价模型预测值和真实值的不一样程度

   两系损失函数：

   

1. 绝对值loss

   • $L(Y,f(x))=|Y-f(x)|$
   • 
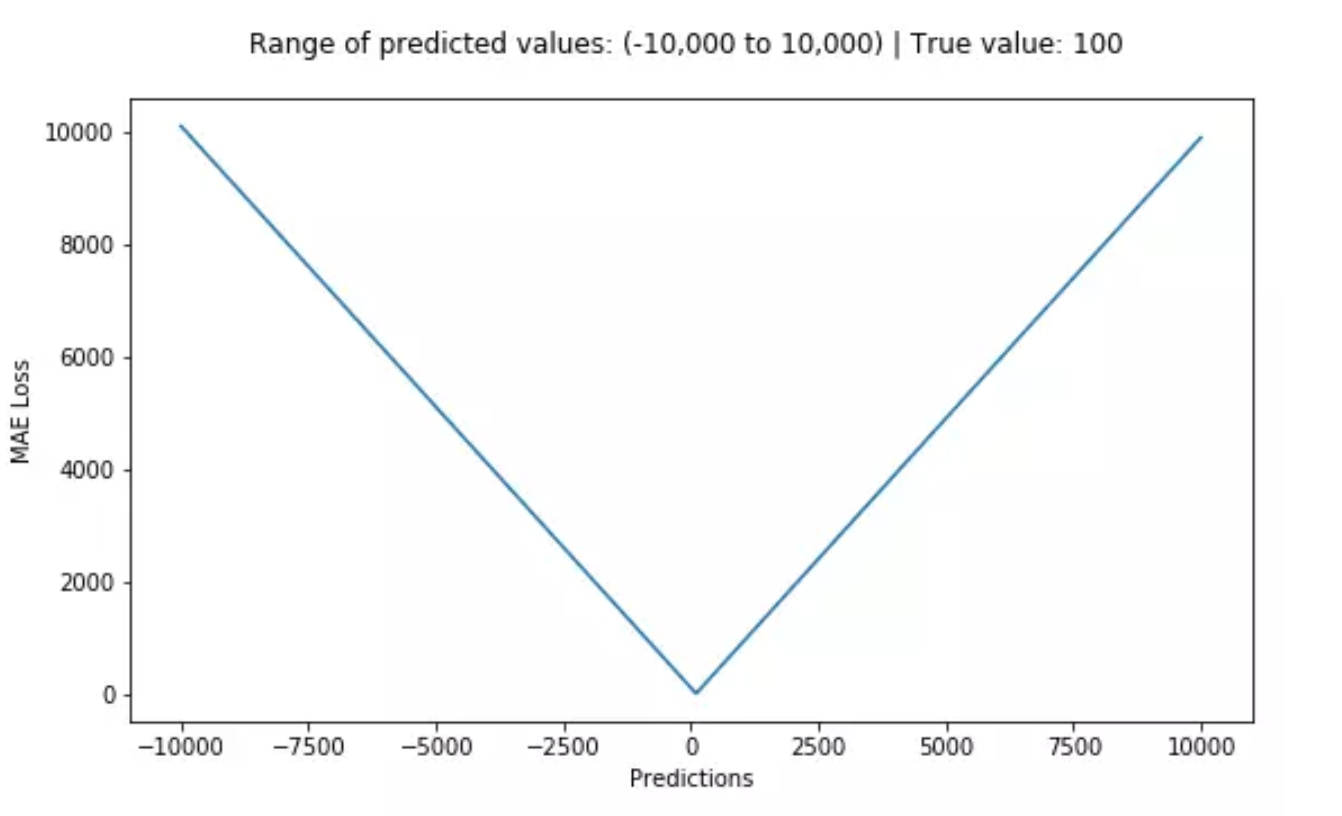
   • 平均绝对值损失，MAE，L1
   • 对异常点有更好的鲁棒性
   • 更新的梯度始终相同，对于很小的损失值，梯度也很大，不利于模型学习——手动衰减学习率

2. 平方差loss

   • $L(Y, f(x)) = (Y-f(x))^2$
   • 
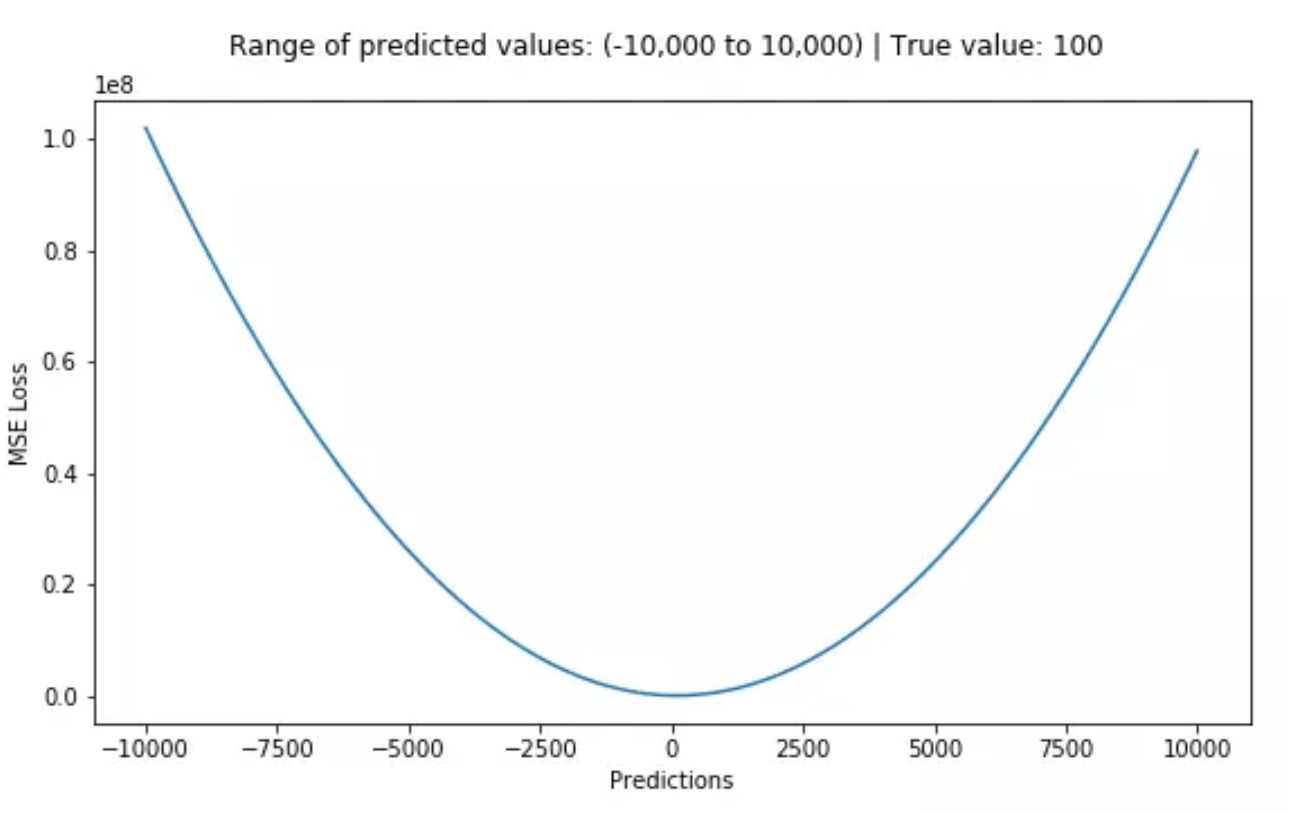
   • 均方误差损失，MSE，L2
   • 因为取了平方，会赋予异常点更大的权重，会以牺牲其他样本的误差为代价，朝着减小异常点误差的方向更新，降低模型的整体性能

3. Huber loss

   • $L = \begin{cases} \frac{1}{2}(y-f(x))^2,\text{ for }|y-f(x)|<\delta,\\ \delta |y-f(x)|-\frac{1}{2}\delta^2, \text{ otherwise} \end{cases} $
   • 
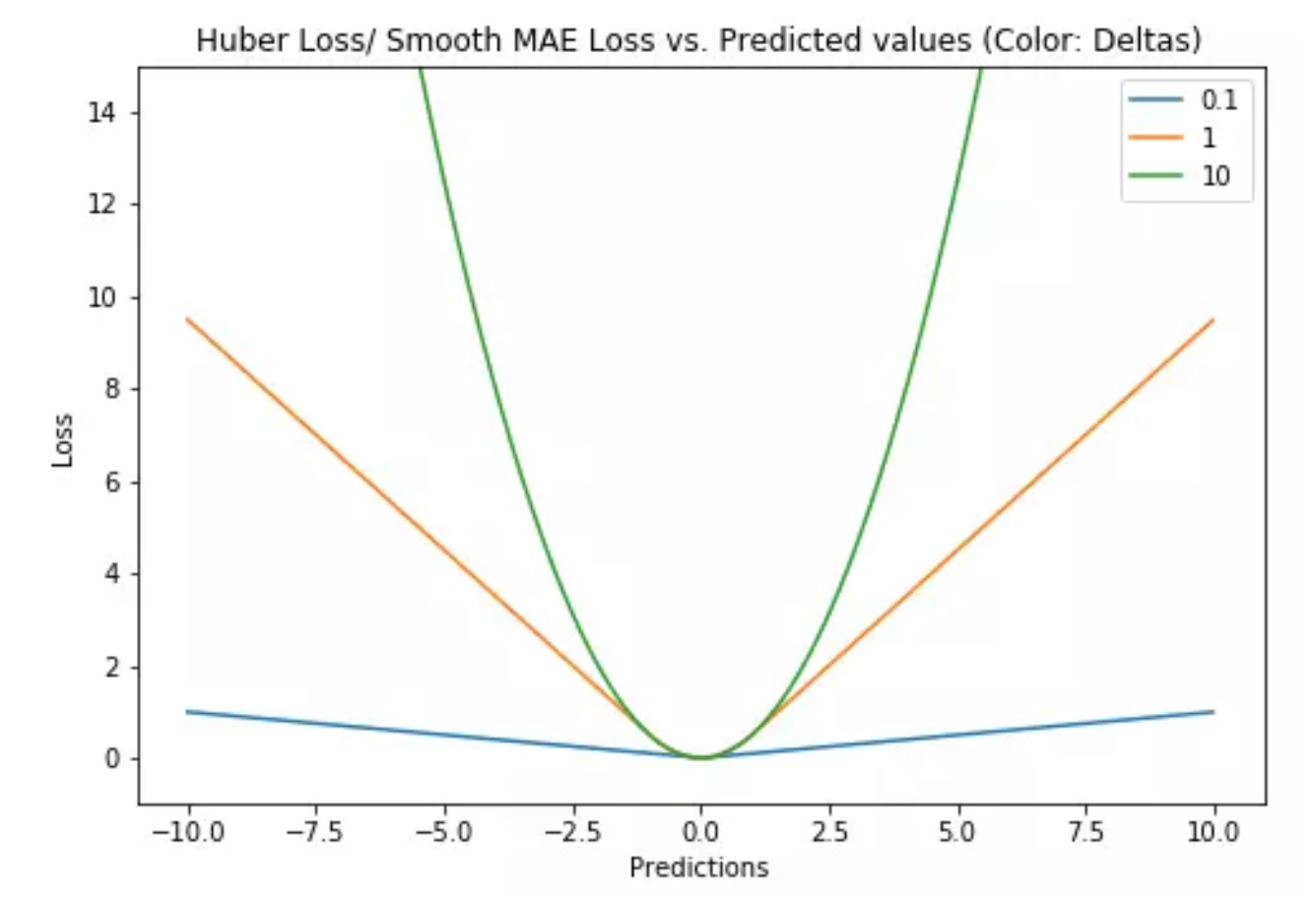
   • 超参决定了对与异常点的定义，只对较小的异常值敏感

4. 对数loss

   $$L(Y, P(Y|X)) = -log(P(Y|X))$$

5. cross-entropy loss

   二分类双边计算：

   $$L = ylna + (1-y)ln(1-a)$$

   多分类单边计算：

   $$L = ylna$$

1. 指数loss

   $$L(Y, f(x)) = exp[-yf(x)]$$

2. Hinge loss

   $$L(Y, f(x)) = max(0, 1-yf(x))$$

3. perceptron loss

   $$L(Y, f(x)) = max(0, -yf(x))$$

4. cross-entropy loss

   二分类双边计算：

   $$L = ylna + (1-y)ln(1-a)$$

   多分类单边计算：

   $$L = ylna$$