reference: https://bbs.cvmart.net/articles/1396
IoU
IoU = Intersection / Union
$Loss_{IoU} = 1 - IoU$
- [0,1]
- 无法直接优化没有重叠的部分:如果两个框没有交集,IoU=0,没有梯度回传,无法进行学习训练
- 尺度不敏感
无法精确的反映两者的重合质量
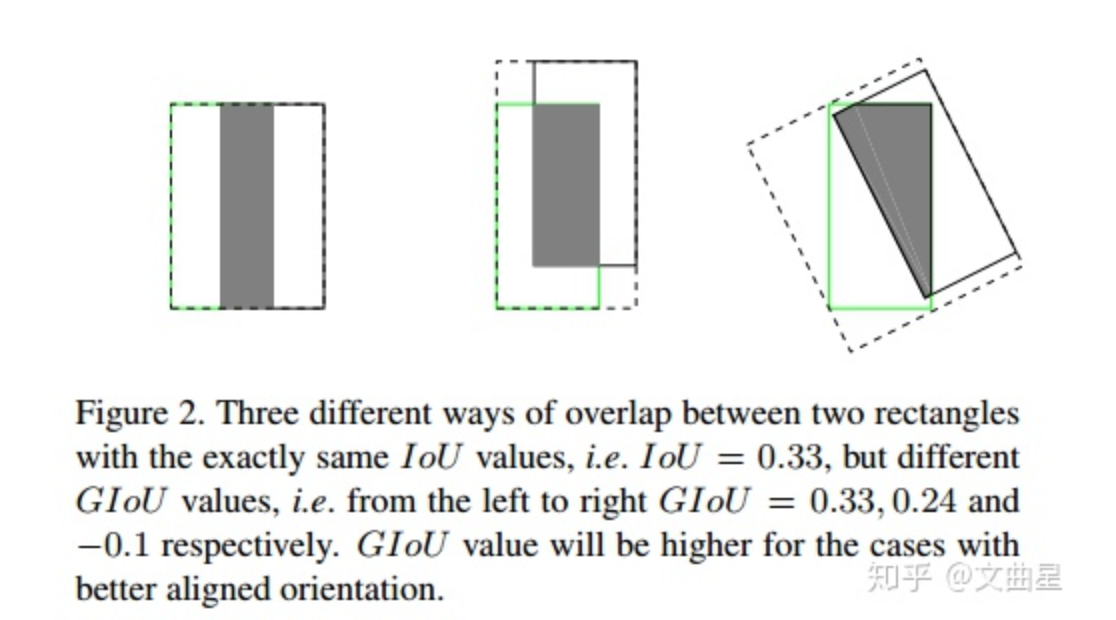
GIoU(Generalized Intersection over Union)
$GIoU = IoU - \frac{|A_c - U|}{|A_c|}$,$A_c$是包含两个框的最小外接框
$Loss_{GIoU} = 1 - GIoU$
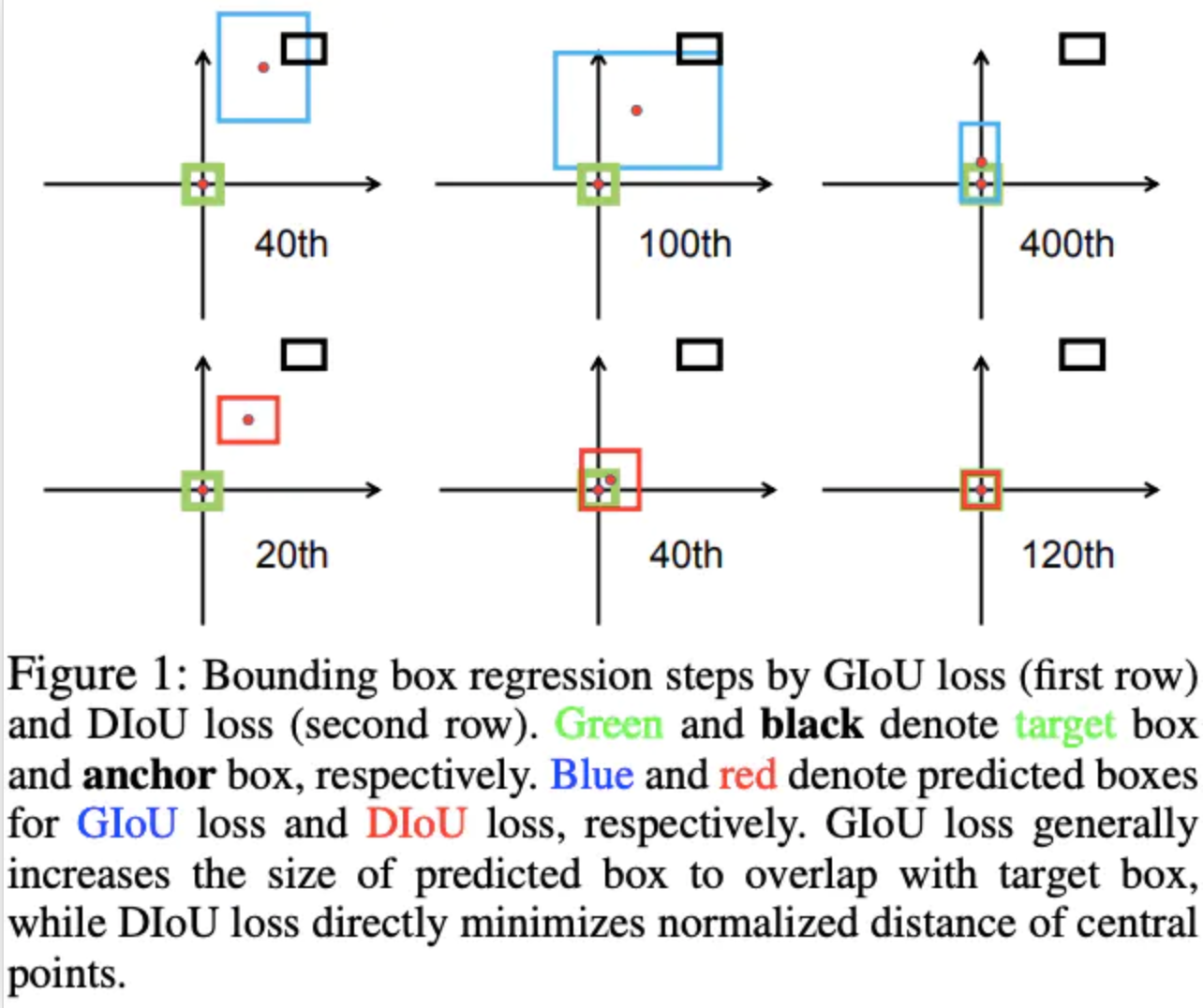
- GIoU倾向于先增大bbox的大小来增大与GT的交集,然后通过IoU项引导最大化bbox的重叠区域
- [-1,1]:对称区间
- 能够关注到非重合区域:引入了外接框C
- 尺度不敏感
- 两个框为包含关系时,退化为IoU
- 如果之间用来替换mse,前期收敛会比较慢
- 一般地,GIoU loss不能很好地收敛SOTA算法,反而造成不好的结果
DIoU (Distance-IoU)
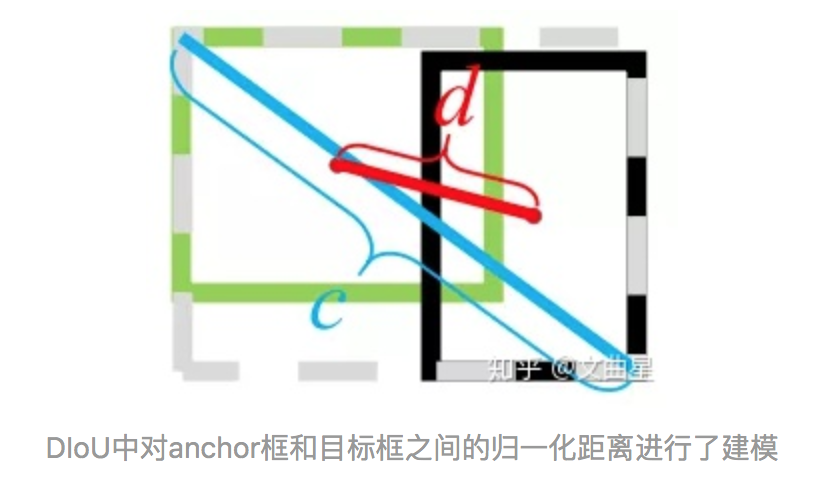
$DIoU = IoU - \frac{d^2}{c^2}$,d是两个中心点间的欧式距离,c是两个框的最小外接框的对角线距离
$Loss_{DIoU} = 1 - DIoU$
* 直接最小化两个目标框的距离,收敛快得多,而且稳定
* 也能够关注到非重合区域:引入外接对角线
* 对于包含关系的两个框,仍旧有距离损失,不会退化为IoU:因为中心点距离
* 可以替换NMS中的IoU:原始的IoU仅考虑了重叠区域,对包含的情况没有很好的处理
$$
score = score\text{ if }IoU - dis(box_{max}, box)>\epsilon \text{, else } 0
$$
* 没有考虑形状(长宽比)
CIoU (Complete-IoU)
$CIoU = IoU - \frac{d^2}{c^2}-av$,在DIoU的基础上新增了惩罚项av,a是权重系数,v用来评价长宽比:
$Loss_{CIoU} = 1 - CIoU$
v的梯度中有$\frac{1}{w^2+h^2}$,长宽在[0,1]之间,可能很小,会导致梯度爆炸,用的时候
- clamp一下上下限
分母中的$w^2+h^2$替换成1