PolarMask: Single Shot Instance Segmentation with Polar Representation
动机
- instance segmentation
- anchor-free
- single-shot
- modified on FCOS
论点
- two-stage methods
- FCIS, Mask R-CNN
- bounding box detection then semantic segmentation within each box
- single-shot method
- formulate the task as instance center classification and dense distance regression in a polar coordinate
- FCOS can be regarded as a special case that the contours has only 4 directions
this paper
- two parallel task:
- instance center classification
- dense distance regression
- Polar IoU Loss can largely ease the optimization and considerably improve the accuary
- Polar Centerness improves the original idea of “Centreness” in FCOS, leading to further performance boost
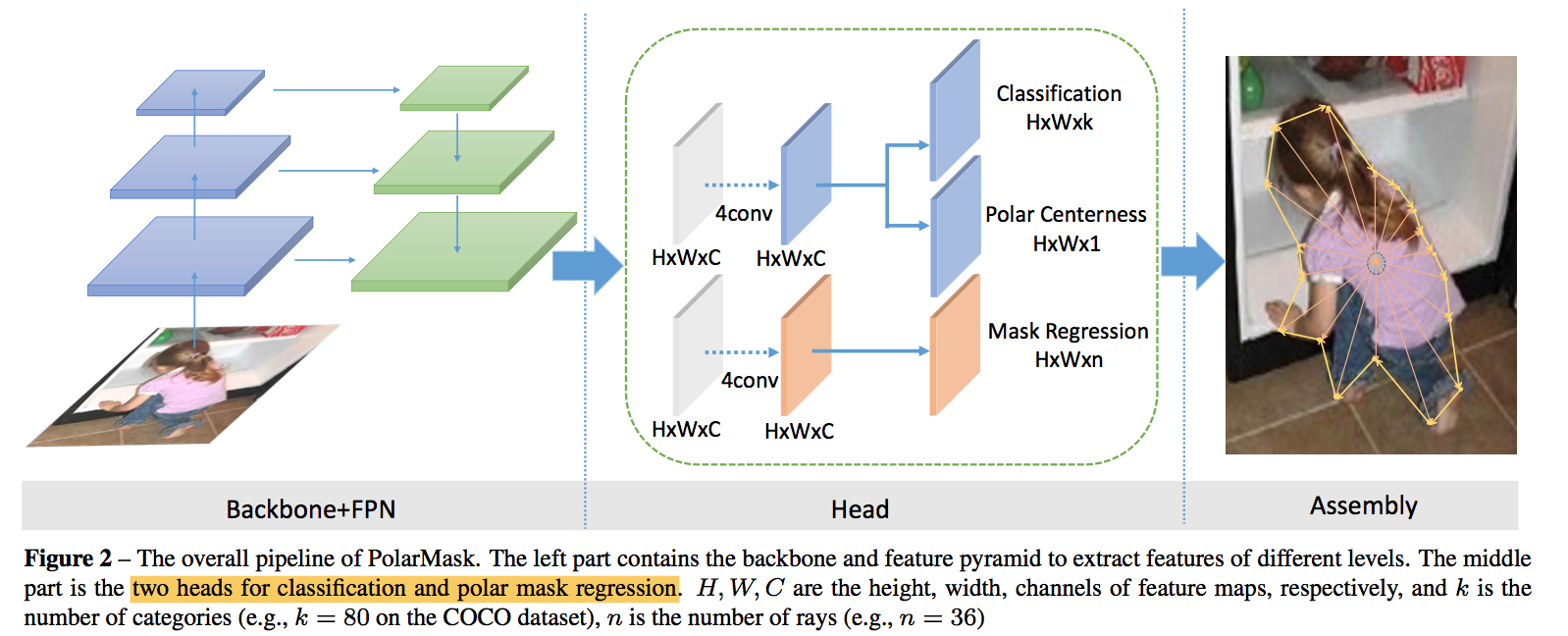
- two parallel task:
- two-stage methods
方法
- architecture
- back & fpn are the same as FCOS
- model the instance mask as one center and n rays
- conclude that mass-center is more advantageous than box center
- the angle interval is pre-fixed, thus only the length of the rays is to be regressed
- positive samples:falls into 1.5xstrides of the area around the gt mass-center,that is 9-16 pixels around gt grid
- distance regression
- 如果一条射线上存在多个交点,取最长的
- 如果一条射线上没有交点,取最小值$\epsilon=10^{-6}$
- potential issuse of the mask regression branch
- dense regression task with such as 36 rays, may cause imbalance between regression loss and classification loss
- n rays are relevant and should be trained as a whole rather than a set of independent values—->iou loss
- inference
- multiply center-ness with classification to obtain final confidence scores, conf thresh=0.05
- take top-1k predictions per fpn level
- use the smallest bounding boxes to run NMS, nms thresh=0.5
- polar centerness
- to suppress low quality detected centers
- $polar\ centerness=\sqrt{\frac{min(\{d_1,d_2, …, d_n\})}{max(\{d_1,d_2, …, d_n\})}}$
- $d_{min}$和$d_{max}$越接近,说明中心点质量越好
- Experiments show that Polar Centerness improves accuracy especially under stricter localization metrics, such as $AP_{75}$
- polar IoU loss
- polar IoU:$IoU=lim_{N\to\inf}\frac{\sum_{i=1}^N\frac{1}{2} d_{min}^2 \Delta \theta}{\sum_{i=1}^N\frac{1}{2} d_{max}^2 \Delta \theta}$
- empirically observe that 去掉平方项效果更好:$polar\ IoU=\frac{\sum_{i=1}^n d_{min}}{\sum_{i=1}^n d_{max}}$
- polar iou loss:bce of polar IoU,$-log(\frac{\sum_{i=1}^n d_{min}}{\sum_{i=1}^n d_{max}})$
- advantage
- differentiable, enable bp
- regards the regression targets as a whole
- keep balance with classification loss
- architecture