FCOS: Fully Convolutional One-Stage Object Detection
动机
- anchor free
- proposal free
- avoids the complicated computation related to anchor boxes
- calculating overlapping during training
- avoid all hyper-parameters related to anchor boxes
- size & shape
- positive/ignored/negative
- leverage as many foreground samples as possible
论点
anchor-based detectors
- detection performance is sensitive to anchor settings
- encounter difficulties in cases with large shape variations
- hamper the generalization ability of detectors
- dense propose:the excessive number of negative samples aggravates the imbalance
- involve complicated computation:such as calculating the IoU with gt boxes
FCN-based detector
- predict a 4D vector plus a class category at each spatial location on a level of feature maps
- do not work well when applied to overlapped bounding boxes
with FPN this ambiguity can be largely eliminated

anchor-free detector
- yolov1:only the points near the center are used,low recall
- CornerNet:complicated post-processing to match the pairs of corners
- DenseBox:difficulty in handling overlapping bounding boxes
this methos
- use FPN to deal with ambiguity
- dense predict:use all points in a ground truth bounding box to predict the bounding box
- introduce “center-ness” branch to predict the deviation of a pixel to the center of its corresponding bounding box
- can be used as a RPN in two-stage detectors and can achieve significantly better performance
方法
ground truth boxes,$B_i=(x_0, y_0, x_1, y_1, c)$,corners + cls
anchor-free:each location (x,y),map into abs input image (xs+[s/2], ys+[s/2])
positive sample:if a location falls into any ground-truth box
ambiguous sample:location falls into multiple gt boxes,choose the box with minimal area
regression target:l t r b distance,location to the four sides
cls branch
- C binary classifiers
- C-dims vector p
- focal loss
- $\frac{1}{N_{pos}} \sum_{x,y}L_{cls}(p_{x,y}, c_{x,y}^*)$
calculate on both positive/negative samples
box reg branch
- 4-dims vector t
- IOU loss
- $\frac{1}{N_{pos}} \sum_{x,y}1_{\{c_{x,y}^>0\}}L_{reg}(t_{x,y}, t_{x,y}^)$
- calculate on positive samples
inference
choose the location with p > 0.05 as positive samples
two possible issues
- large stride makes BPR low, which is actually not a problem in FCOS
overlaps gt boxes cause ambiguity, which can be greatly resolved with multi-level prediction
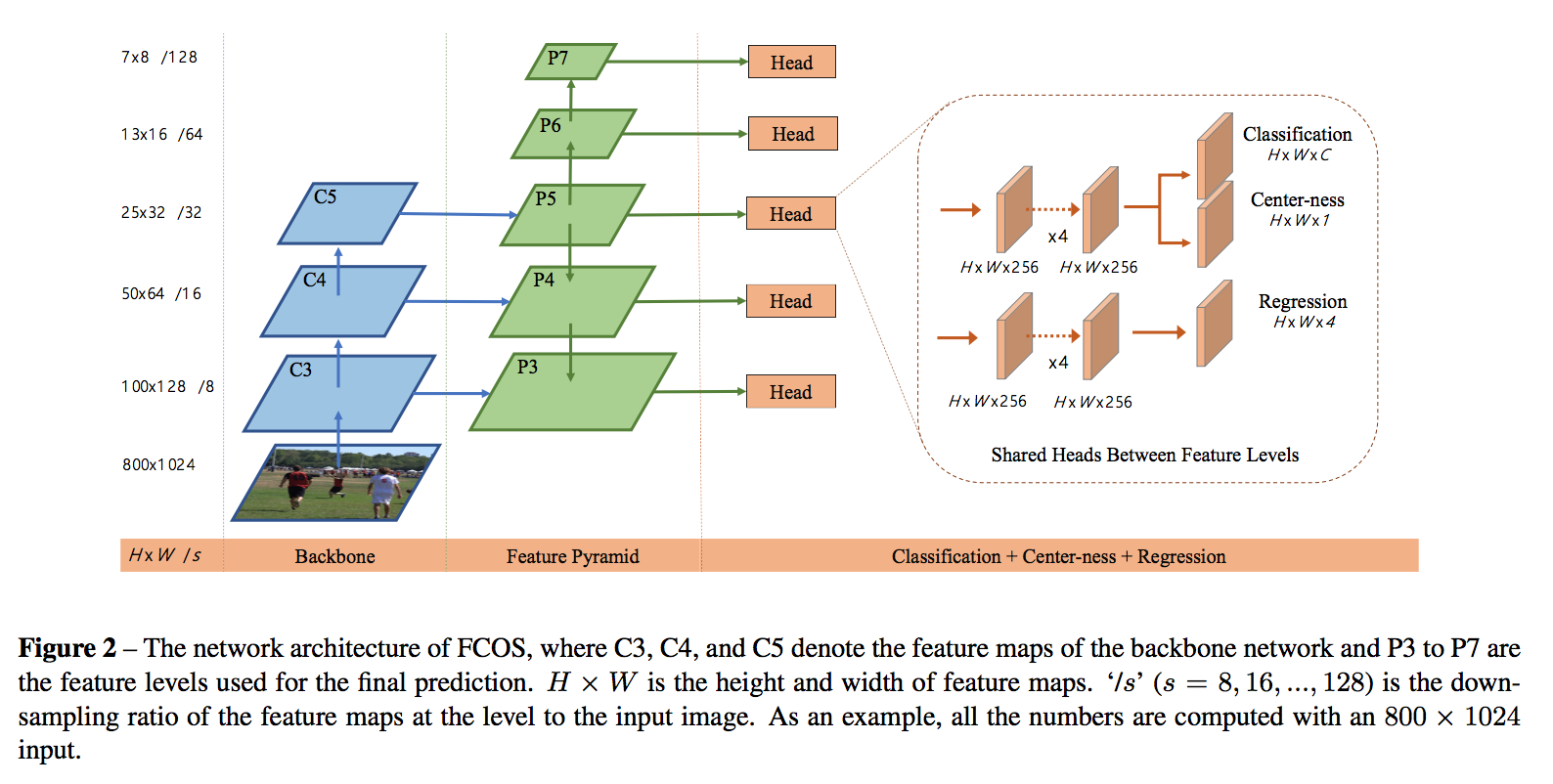
FPN
- P3, P4, P5:1x1 conv from C3, C4, C5, top-down connections
P6, P7: stride2 conv from P5, P6
limit the bbox regression for each level
- $m_i$:maximum distance for each level
- if a location’s gt bbox satifies:$max(l^,t^,r^,b^)>m_i$ or $max(l^,t^,r^,b^)<m_{i-1}$,it is set as a negative sample,not regress at current level
- objects with different sizes are assigned to different feature levels:largely alleviate一部分box overlapping问题
for other overlapping cases:simply choose the gt box with minimal area
sharing heads between different feature levels
to regress different size range:use $exp(s_ix)$
- trainable scalar $s_i$
- slightly improve
center-ness
low-quality predicted bounding boxes are produced by locations far away from the center of an object
predict the “center-ness” of a location
normalized distance
sqrt to slow down the decay
[0,1] use bce loss
when inference center-ness is mutiplied with the class score:can down-weight the scores of bounding boxes far from the center of an object, then filtered out by NMS
- an alternative of the center-ness:use of only the central portion of ground-truth bounding box as positive samples,实验证明两种方法结合效果最好
architecture
- two minor differences from the standard RetinaNet
- use Group Normalization in the newly added convolutional layers except for the last prediction layers
- use P5 instead of C5 to produce P6&P7
- two minor differences from the standard RetinaNet