group normalization

Group Normalization

1. 动机

   • for small batch size
   • do normalization in channel groups
   • batch-independent
   • behaves stably over different batch sizes
   • approach BN’s accuracy

   

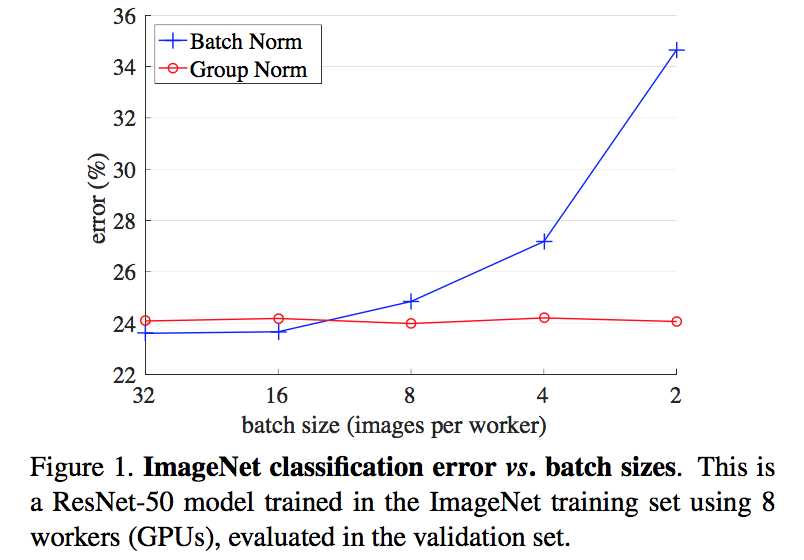
2. 论点

   • BN
     • requires sufficiently large batch size (e.g. 32)
     • Mask R-CNN frameworks use a batch size of 1 or 2 images because of higher resolution, where BN is “frozen” by transforming to a linear layer
     • synchronized BN 、BR
   • LN & IN
     • effective for training sequential models or generative models
     • but have limited success in visual recognition
     • GN能转换成LN／IN
   • WN
     • normalize the filter weights, instead of operating on features

3. 方法

   • group

     • it is not necessary to think of deep neural network features as unstructured vectors
       • 第一层卷积核通常存在一组对称的filter，这样就能捕获到相似特征
       • 这些特征对应的channel can be normalized together

   • normalization

     • transform the feature x：$\hat x_i = \frac{1}{\sigma}(x_i-\mu_i)$

     • the mean and the standard deviation：

       $$\mu_i=\frac{1}{m}\sum_{k\in S_i}x_k\\ \sigma_i=\sqrt {\frac{1}{m}\sum_{k\in S_i}(x_k-\mu_i)^2+\epsilon}$$

     • the set $S_i$

       • BN：
         • $S_i=\{k|k_C = i_C\}$
         • pixels sharing the same channel index are normalized together
         • for each channel, BN computes μ and σ along the (N, H, W) axes
       • LN
         • $S_i=\{k|k_N = i_N\}$
         • pixels sharing the same batch index (per sample) are normalized together
         • LN computes μ and σ along the (C,H,W) axes for each sample
       • IN
         • $S_i=\{k|k_N = i_N, k_C=i_C\}$
         • pixels sharing the same batch index and the same channel index are normalized together
         • LN computes μ and σ along the (H,W) axes for each sample
       • GN
         • $S_i=\{k|k_N = i_N, [\frac{k_C}{C/G}]=[\frac{i_C}{C/G}]\}$
         • computes μ and σ along the (H, W ) axes and along a group of C/G channels

     • linear transform

       • to keep representational ability
       • per channel
       • scale and shift：$y_i = \gamma \hat x_i + \beta$

       

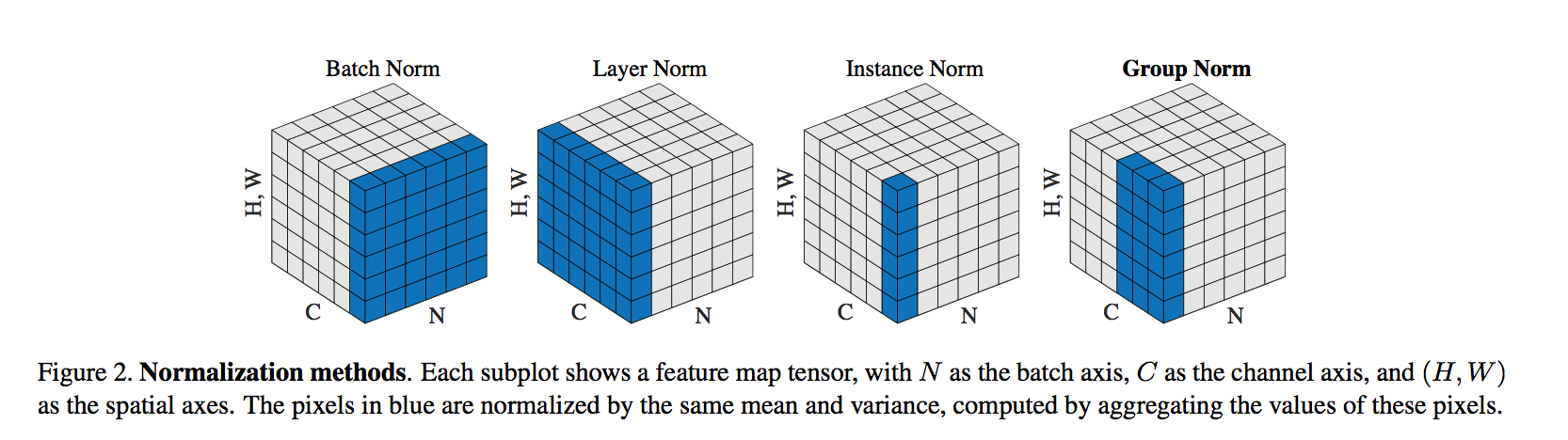
   • relation

     • to LN
       • LN assumes all channels in a layer make “similar contributions”
       • which is less valid with the presence of convolutions
       • GN improved representational power over LN
     • to IN
       • IN can only rely on the spatial dimension for computing the mean and variance
       • it misses the opportunity of exploiting the channel dependence
       • 【QUESTION】BN也没考虑通道间的联系啊，但是计算mean和variance时跨了sample

   • implementation

     • reshape
     • learnable $\gamma \& \beta$
     • computable mean & var

   

4. 实验

   • GN相比于BN，training error更低，但是val error略高于BN
     • GN is effective for easing optimization
     • loses some regularization ability
     • it is possible that GN combined with a suitable regularizer will improve results
   • 选取不同的group数，所有的group>1均好于group=1（LN）
   • 选取不同的channel数（C／G），所有的channel>1均好于channel=1（IN）
   • Object Detection
     • frozen：因为higher resolution，batch size通常设置为2/GPU，这时的BN frozen成一个线性层$y=\gamma(x-\mu)/\sigma+beta$，其中的$\mu$和$sigma$是load了pre-trained model中保存的值，并且frozen掉，不再更新
     • denote as BN*
     • replace BN* with GN during fine-tuning
     • use a weight decay of 0 for the γ and β parameters