SQUEEZENET: ALEXNET-LEVEL ACCURACY WITH 50X FEWER PARAMETERS AND <0.5MB MODEL SIZE
动机
- Smaller CNN
- achieve AlexNet-level accuracy
- model compression
论点
- model compression
- SVD
- sparse matrix
- quantization (to 8 bits or less)
- CNN microarchitecture
- extensively 3x3 filters
- 1x1 filters
- higher level building blocks
- bypass connections
- automated designing approaches
- this paper eschew automated approaches
- propose and evaluate the SqueezeNet architecture with and without model compression
- explore the impact of design choices
- model compression
方法
architectural design strategy
- Replace 3x3 filters with 1x1 filters
- Decrease the number of input channels to 3x3 filters (squeeze)
- Downsample late in the network so that convolution layers have large activation maps:large activation maps (due to delayed downsampling) can lead to higher classification accuracy
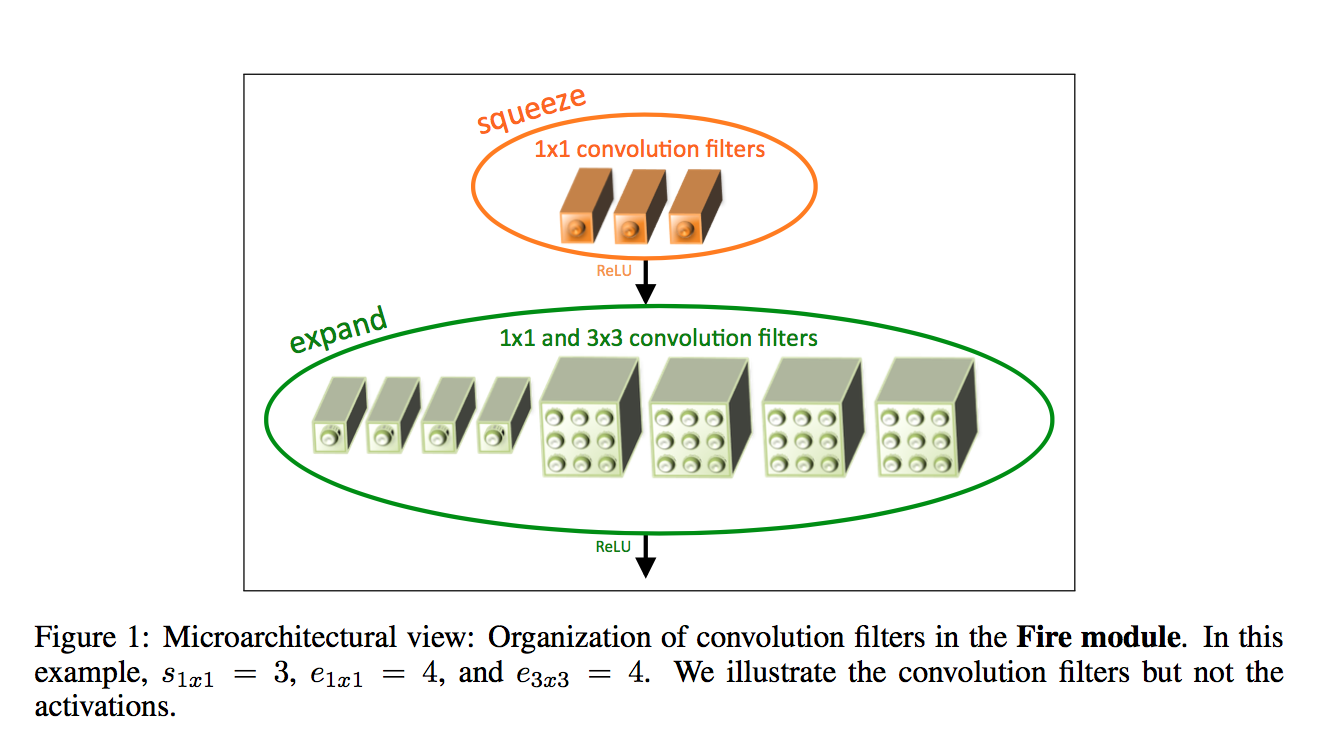
the fire module
- squeeze:1x1 convs
- expand:mix of 1x1 and 3x3 convs, same padding
- relu
concatenate
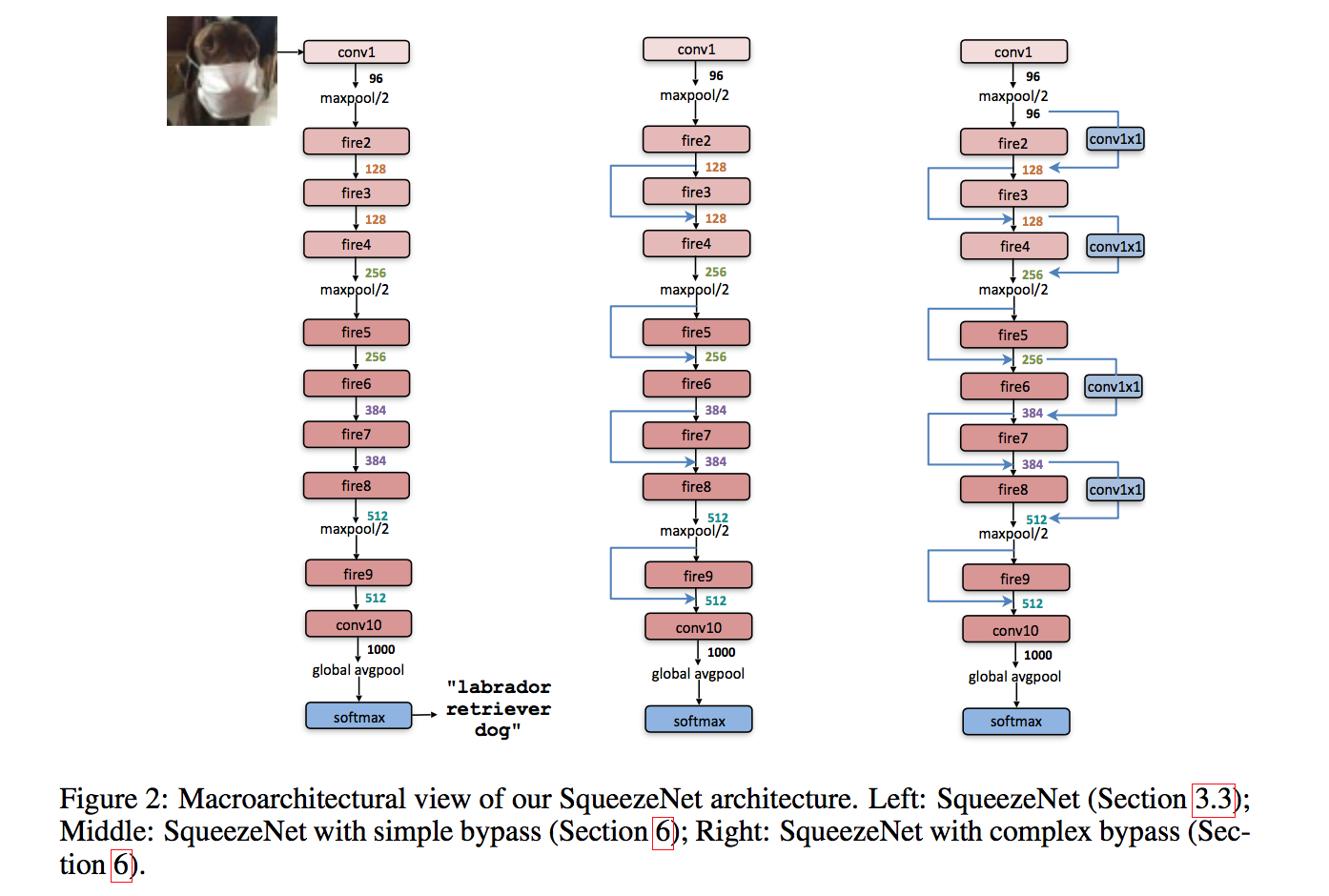
the SqueezeNet
- a standalone convolution layer (conv1)
- followed by 8 Fire modules (fire2-9)
- ending with a final conv layer (conv10)
- stride2 max-pooling after layers conv1, fire4, fire8, and conv10
- dropout with a ratio of 50% is applied after the fire9 module
GAP
understand the impact
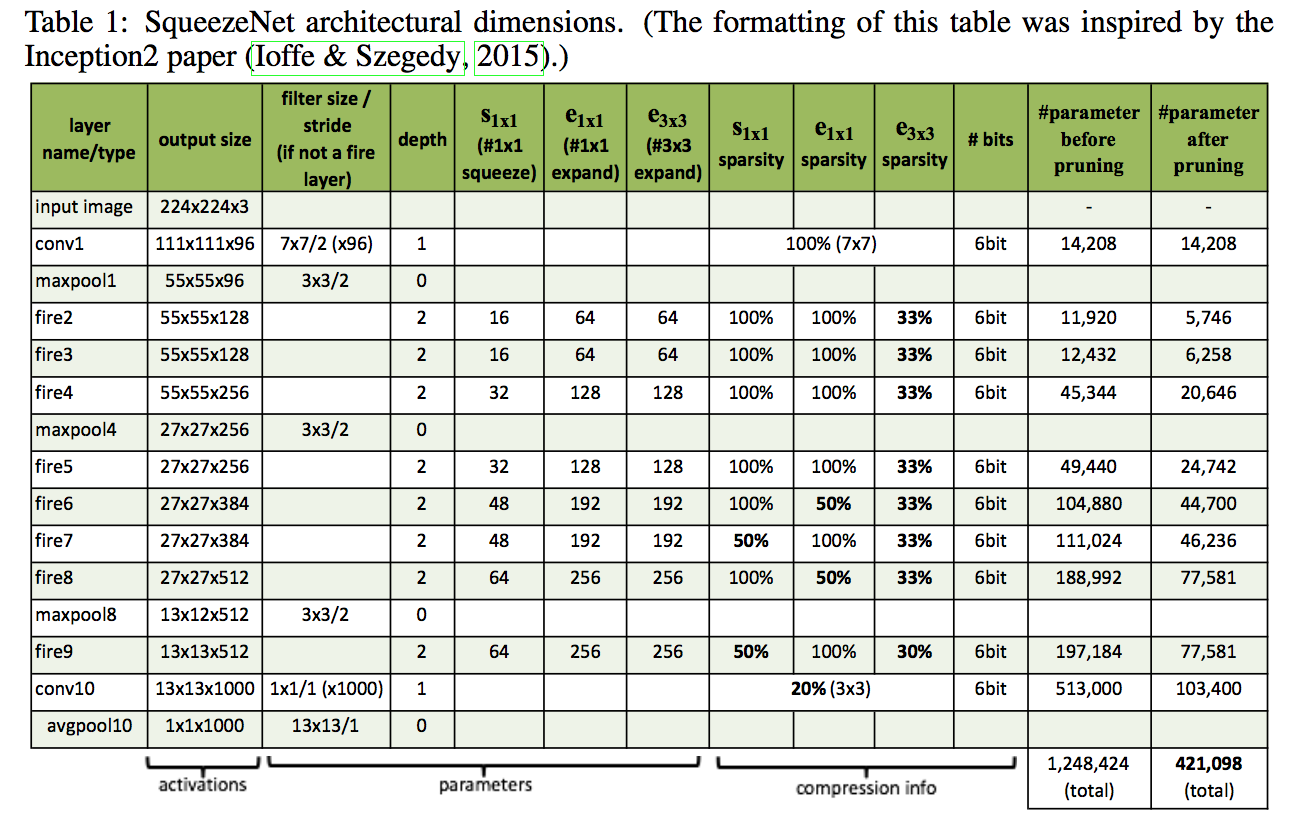
each Fire module has three dimensional hyperparameters, to simplify:
- define $base_e$:the number of expand filters in the first Fire module
- for layer i:$e_i=base_e + (incr_e*[\frac{i}{freq}])$
- expand ratio $pct_{3x3}$:the percentage of 3x3 filters in expand layers
- squeeze ratio $SR$:the number of filters in the squeeze layer/the number of filters in the expnad layer
- normal setting:$base_e=128, incre_e=128, pct_{3x3}=0.5, freq=2, SR=0.125$
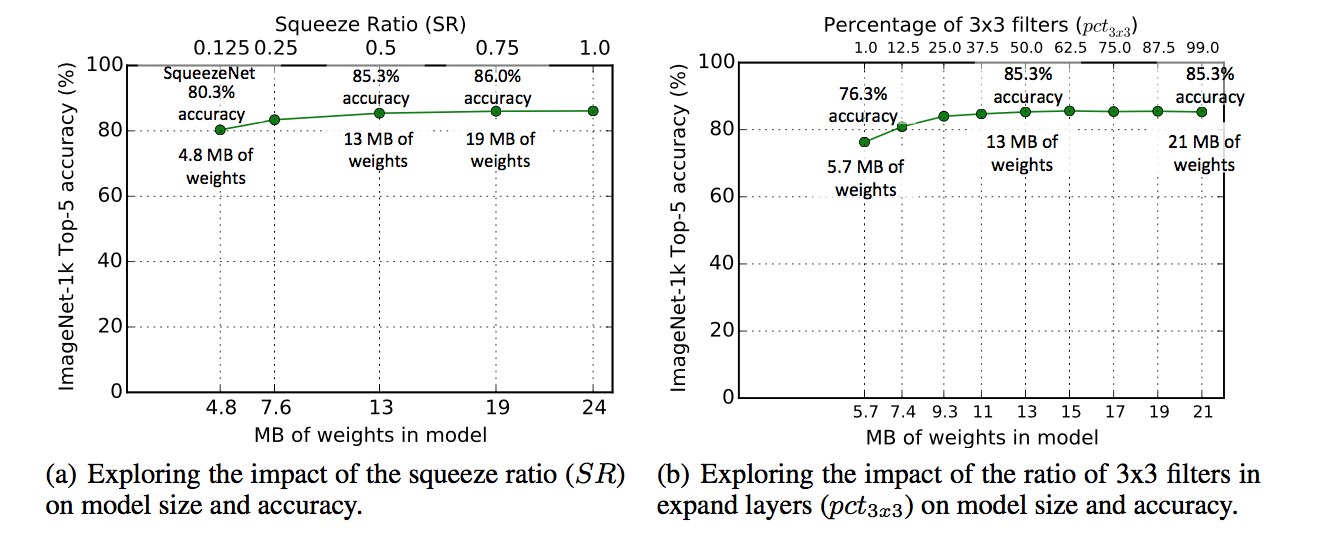
SR
- increasing SR leads to higher accuracy and larger model size
- Accuracy plateaus at 86.0% with SR=0.75
- further increasing provides no improvement
pct
- increasing pct leads to higher accuracy and larger model size
- Accuracy plateaus at 85.6% with pct=50%
- further increasing provides no improvement
bypass
- Vanilla
- simple bypass:when in & out channels have the same dimensions
- complex bypass:includes a 1x1 convolution layer
- alleviate the representational bottleneck introduced by squeeze layers
- both yielded accuracy improvements
- simple bypass enabled higher accuracy