Hausdorff Distance

Reducing the Hausdorff Distance in Medical Image Segmentation with Convolutional Neural Networks

1. 动机

   • novel loss function to reduce HD directly
   • propose three methods
   • 2D&3D，ultra & MR & CT
   • lead to approximately 18 − 45% reduction in HD without degrading other segmentation performance criteria

2. 论点

   • HD is one of the most informative and useful criteria because it is an indicator of the largest segmentation error
   • current segmentation algorithms rarely aim at minimizing or reducing HD directly
     • HD is determined solely by the largest error instead of the overall segmentation performance
     • HD‘s sensitivity to noise and outliers —> modified version
     • the optimization diffculty
   • thus we propose an “HD- inspired” loss function

3. 方法

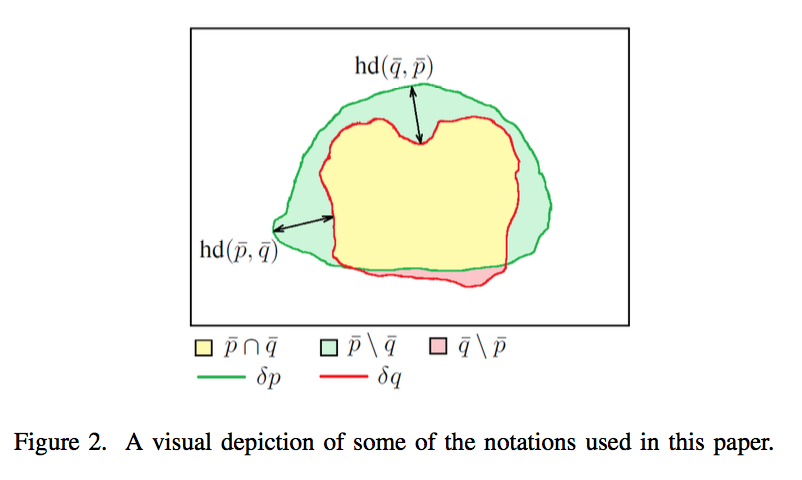
   • denotations

     • probability：$q$
     • binary mask：$\bar p$、$\bar q$
     • boundary：$\delta p$、$\delta q$

     • single hd：$hd(\bar p, \bar q)$、$hd(\bar q, \bar p)$

       

   • based on distance transforms

     • distance map $d_p$：define the distance map as the unsigned distance to the boundary $\delta p$

       $$DT_X[i,j] = min_{[k,l]\in X}d([i,j], [k,l])$$

       距离场定义为：每个点到目标区域(X)的距离的最小值

       

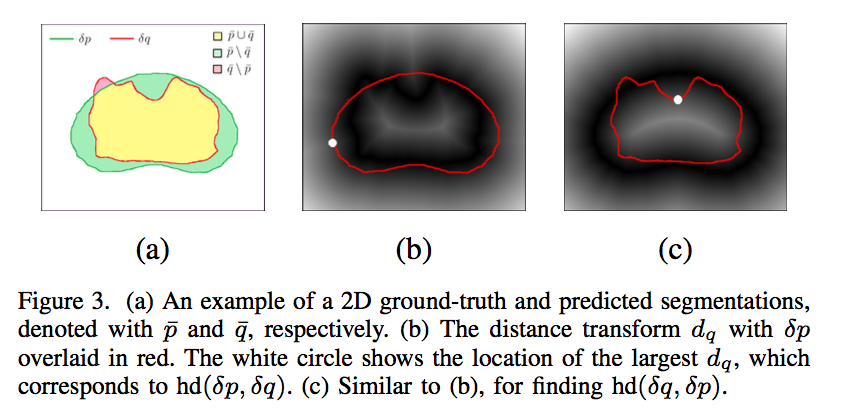
     • HD based on DT：

       $$hd_{DT}(\delta p, \delta q) = max((\bar p \triangle \bar q)\circ d_p)\\ \bar p \triangle \bar q = |\bar p - \bar q|$$
       • finally have： $$HD_{DT}(\delta p, \delta q) = max(hd_{DT}(\delta p, \delta q), hd_{DT}(\delta q, \delta p))$$

     • modified loss version of HD：

       $$Loss_{DT}(q,p) = \frac{1}{|\Omega|}\sum_{\Omega}((p-q)^2\circ(d_p^{\alpha}+d_q^{\alpha}))$$
       • penalizely focus on areas instead of single point
       • $\alpha$ determines how strongly we penalize larger errors
       • use possibility instead of thresholded value
       • use $(p-q)^2$ instead of $|p-q|$

     • correlations

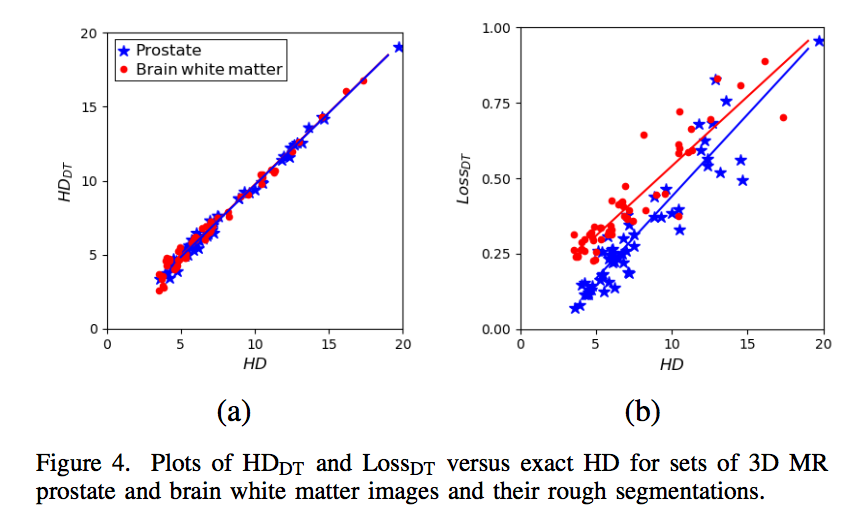
       • $HD_{DT}$：Pearson correlation coefficient above 0.99

       • $Loss_{DT}$：Pearson correlation coefficient above 0.93

         

     • drawback

       • high computational cost especially in 3D

       • $q$ changes along with training process thus $d_q$ changes while $d_p$ remains

       • modified one-sided HD (OS)：

         $$Loss_{DT-OS}(q,p) = \frac{1}{|\Omega|}\sum_{\Omega}((p-q)^2\circ(d_p^{\alpha}))$$

   • HD using Morphological Operations

     • morphological erosion：

       $$S \ominus B = \{z\in \Omega | B(z) \subseteq S\}$$

       腐蚀操作定义为：在原始二值化图的前景区域，以每个像素为中心点，run structure element block B，如果B完全在原图内，则当前中心点在腐蚀后也是前景。

     • HD based on erosion：

       $$HD_{ER}(\delta p, \delta q)=2r^*\\ where\ r^* = min_r \{(\bar p \triangle \bar q) \ominus B_r = \varnothing\}$$
       • $HD_{ER}$ is a lower bound of the true value
       • can be computed more efficiently using convolutional operations

     • modifid loss version：

       $$Loss_{ER}(q,p) = \frac{1}{|\Omega|}\sum_k \sum_{\Omega}((p-q)^2 \ominus_k B)k^{\alpha}$$
       • k successive erosions
       • cross-shaped kernel whose elements sum to one followed by a soft thresholding at 0.50

     • correlations

       • $HD_{ER}$：Pearson correlation coefficient above 0.91
       • $Loss_{ER}$：Pearson correlation coefficient above 0.83

   • HD using circular-shaped convolutional kernel

     • circular-shaped kernel

       

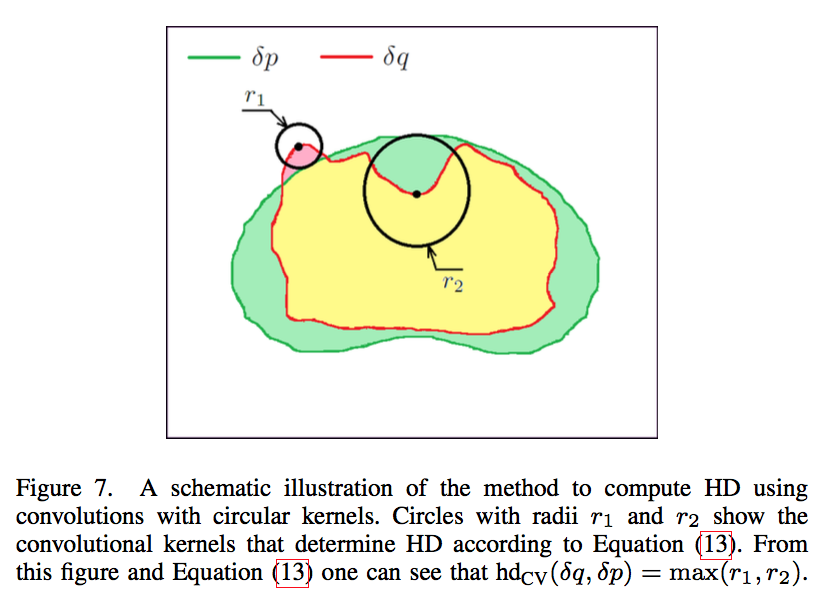
     • HD based on circular-shaped kernel：

       $$hd_{CV}(\delta p, \delta q)=max(r_1, r_2)\\ where \ r_1=max_r (max_{\Omega}f_h(\bar p ^C * B_r)\circ(\bar q \backslash \bar p))\\ where \ r_2=max_r (max_{\Omega}f_h(\bar p * B_r)\circ(\bar p \backslash \bar q))\\$$
       • $\bar p^C$：complement 补集
       • $f_h$：hard thresholding setting all values below 1 to zero

     • modified loss version：

       $$Loss_{CV}(q,p)=\frac{1}{|\Omega|}\sum_{r\in R}r^{\alpha}\sum_{\Omega}[f_s(Br*\bar p^C)\circ f_{\bar q\backslash \bar p} + f_s(B_r * \bar p) \circ f_{\bar p \backslash \bar q}\\ +f_s(Br*\bar q^C)\circ f_{\bar p\backslash \bar q} + f_s(B_r * \bar q) \circ f_{\bar q \backslash \bar p}]$$
       • soft thresholding
       • $$f_{\bar p\backslash \bar q} = (p-q)^2*p$$

     • correlations

       • $HD_{CV}$：Pearson correlation coefficient above 0.99
       • $Loss_{CV}$：Pearson correlation coefficient above 0.88

     • computation：

       • kernel size
         • $HD_{ER}$ is computed using small fixed convolutional kernels (of size 3)
         • $Loss_{CV}$ require applying filters of increasing size(we use a maximum kernel radius of 18 pixels in 2D and 9 voxels in 3D)
       • steps
         • choose R based on the expected range of segmentation errors
         • set R = {3, 6, . . . 18} for 2D images and R = {3,6,9} for 3D

   • training

     • standard Unet
     • augment our HD-based loss term with a DSC loss term for more stable training
     • reweight both loss after every epoch

d