amcl

滤波：

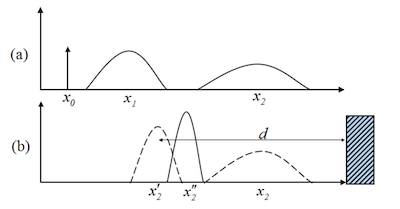
机器人从已知点$x_0$开始运动，里程计误差逐渐累积，位置不确定性将越来越大（$x_1, x_2$）。因此需要借助外部环境信息对自己进行定位，于是引入测量值$d$，计算出当前位置$x_2^{‘}$，再结合预测值$x_2$，得到一个矫正位置$x_2^{‘’}$，使其不确定性降到最小。

贝叶斯滤波：$p(x|z) = \frac{p(z|x)p(x)}{p(z)}$

先验：$p(x_t|u_t, x_{t-1})$，通过预测方程得到

似然：$p(z_t| x_t)$，通过测量方程得到

后验：$p(x_t|z_t)$，通过贝叶斯方程得到

对于一般的非线性、非高斯系统，很难通过上述方法得到后验概率的解析解。

蒙特卡洛采样：

假设能从一个目标分布$p(x)$获得一系列样本$x_1, x2, …, x_N$，那么就能利用这些样本去估计这个分布的某些函数的期望值。

$$E(f(x)) = \int_a^{b}f(x)p(x)dx \approx\frac{f(x_1) + f(x_2) + ... + f(x_N)}{N}$$

蒙特卡洛采样的核心思想就是用均值来代替积分。

假设可以从后验概率中采样到N个样本，那么后验概率可以表示为：

$$\hat p(x_t|z_{1:t}) = \frac{1}{N} \sum_{i=1}^{N}\delta(x_n - x_n^{i}) \approx p(x_t|z_{1:t})$$

粒子滤波：

$$\begin{align} E(f(x)) & \approx \int f(x_n) \hat p(x_t|z_{1:t}) dx \nonumber\\ & = \frac{1}{N}\sum_N f(x_n) \delta(x_n - x_n^{i})\nonumber\\ & = \frac{1}{N}\sum_N f(x_n^{i}) \nonumber \end{align}$$

用采样粒子（服从后验概率）的状态值直接平均作为期望值，这就是粒子滤波。

MCL：蒙特卡洛定位／粒子滤波定位

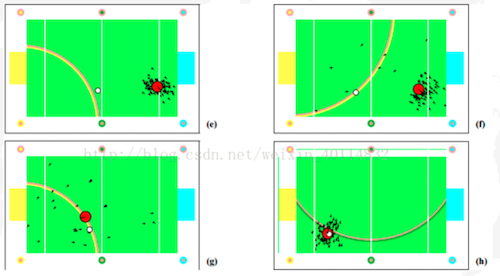
1. Randomly generate a bunch of particles

2. Predict next state of the particles

3. Update the weighting of the particles based on the measurement.

4. Resample：Discard highly improbable particle and replace them with copies of the more probable particles.

   This leads to a new particle set with uniform importance weights, but with an increased number of particles near the three likely places.

5. Compute the weighted mean and covariance of the set of particles to get a state estimate.

权值退化：如果任由粒子权值增长，只有少数粒子的权值较大，其余粒子的权值可以忽略不计，变成无效粒子，因此需要引入重采样。采用$N_{eff}$衡量粒子权值的退化程度。

$$N_{eff} \approx \hat{N_{eff}} = \frac{1}{\sum_N (w_k^{i})^2}$$

粒子多样性：通常我们会舍弃权值较小的粒子，代之以权值较大的粒子。这样会导致权值小的粒子逐渐绝种，粒子群多样性减弱，从而不足以近似表征后验密度。

重要性采样

实际上后验概率并不知道，谈何采样（$x_n^i$）。我们可以从一个已知的分布$q(x|z)$里来采样，间接得到滤波值。

$$\begin{align} E(f(x_k))& = \int f(x) \frac{p(x|z)}{q(x|z)} q(x|z) dx \nonumber\\ & = \frac{E_{q(x|z)}W_k(x_k)f(x_k)}{E_{q(x|z)}W_k(x_k)}\nonumber\\ & \approx \frac{\frac{1}{N} \sum_{i=1}^N W_k({x_k^{i})f(x_k^{i})}}{\frac{1}{N} \sum_{i=1}^N W_k({x_k^{i}})}\nonumber\\ & = \sum_N \hat W_k(x_k^i)f(x_k^i) \nonumber \end{align}$$

相比较于原始的均值表示，变成了加权平均值。不同粒子拥有了不同的权重。

$$\hat W_k(x_k^i) = \frac{W_k(x_k^i)}{\sum_N W_k(x_k^i)}\\ W_k (x_k) \propto \frac{p(x_k|z_{1:k})}{q(x_k|z_{1:k})}$$

已知的$q$分布叫做重要性概率密度函数。

递推算法：序贯重要性采样

$$\{x_k^i, w_k^i\} = SIS(\{x_{k-1}, w_{k-1}\})_{i=1}^N, y_k)$$

首先假设重要性分布$q(x|z)$满足：

$$q(x_k | x_{0:k-1}, y_{1:k}) = q(x_k|x_{k-1}, y_k)$$

即只和前一时刻的状态$x_{k-1}$和测量$y_k$有关。于是有：

$$w_k^i \approx w_{k-1}^i \frac{p(y_k|x_k^i)p(x_k^i|x_{k-1}^i)}{q(x_k^i|x_{k-1}^i, y_k)}$$

伪代码：

For i=1:N
	(1)采样：式1
	(2)权值更新：式2
End For
权值归一化
加权平均得到粒子滤波值，也就是当前状态的估计值
重采样

重采样

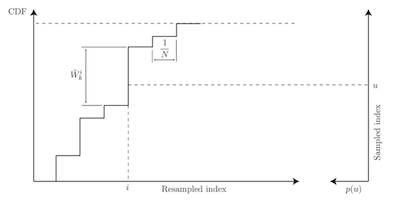
既然权重小的那些粒子不起作用了，那就不要了。为了保持粒子数目不变，就要补充新粒子，最简单的办法就是复制权重大的粒子。用$x_k^i$表示k时刻的粒子，$x_k^j$表示重采样以后的粒子，那么：

$$\tilde p (x_k|y_{1:k}) = \sum_N \frac{1}{N}\delta(x_k - x_k^j) = \sum_N \frac{n_i}{N}\delta(x_k - x_i^j)$$

总的来说，新粒子按照权重比例来补充，算法流程为：

计算概率累积和wcum(N)
用[0,1]之间的均匀分布随机采样N个值u(N)
for i in 1:N:
	k = 1
	while u(i)<wcum(k):
		k += 1
	end while
	resample(i) = k

SIR滤波器（Sampling Importance Resampling Filter ）

选取特定的重要性概率密度函数：

$$q(x_k^i|x_{k-1}^i, y_k) = p(x_k^i|x_{k-1}^i)$$

于是权重更新公式可以简化：

$$w_k^i \propto w_{k-1}^i \frac{p(z|x)p(x|x_{k-1})}{q(x|x_{k-1})}$$

由于重采样以后，粒子分布更新，权值统一为$\frac{1}{N}$，于是权重更新公式进一步简化：

$$w_k^i \propto p(z_k|x_k^i)$$

根据测量方程可知，上面这个概率就是以真实测量值为均值，以噪声方差为方差的高斯分布。

此算法中的采样，并没有加入测量$z_k$，只凭先验知识$p(x_k|x_{k-1})$，虽然简单易用，但是存在效率不高和对奇异点(outliers)敏感的问题。

AMCL

MCL算法能够用于全局定位，但是无法从机器人绑架或全局定位失败中恢复过来，因为随着位置被获取，其他地方的不正确粒子会逐渐消失。稳定状态下，粒子只“生存”在一个单一的姿态附近，如果这个姿态恰好不正确（在重采样步骤中可能意外的丢弃所有正确位姿附近的粒子），算法就无法恢复。

AMCL就是为了解决上述问题：结合了自适应（Augmented_MCL）和库尔贝克-莱不勒散度采样（KLD_Sampling_MCL）

• Augmented_MCL：在机器人遭到绑架的时候，它会在发现粒子们的平均分数突然降低了，这意味着正确的粒子在某次迭代中被抛弃了，此时会随机的全局注入粒子（injection of random particles）。
• KLD_Sampling_MCL：动态调整粒子数，当机器人定位差不多得到了的时候，粒子都集中在一块了，就没必要维持这么多的粒子了——在栅格地图中，看粒子占了多少栅格。占得多，说明粒子很分散，在每次迭代重采样的时候，允许粒子数量的上限高一些。占得少，说明粒子都已经集中了，那就将上限设低。

算法流程上看，augmented_MCL算法最显著的区别就是引入了四个参数用于失效恢复：

• $w_{slow}$：长期似然平均估计
• $w_{fast}$：短期似然平均估计
• $\alpha_{slow}$：长期指数滤波器衰减率
• $\alpha_{fast}$：短期指数滤波器衰减率

失效恢复的核心思想是：测量似然的一个突然衰减（短期似然劣于长期似然）象征着粒子质量的下降，这将引起随机采样数目的增加。

$w_{avg}$计算了粒子的平均权重，当粒子质量下降时，平均权重随之下降，$w_{slow}、w_{fast}$也会随之下降，但是显然$w_{fast}$下降的速度要快于$w_{slow}$——这由衰减率决定，因此随机概率$p = 1 - \frac{w_{fast}}{w_{slow}}$会增大，随机粒子数目增加。而当粒子质量提高时，粒子短期权重要好于长期，随机概率小于0，不生成随机粒子。

ROS amcl参数解析

Augmented_MCL：

• <param name="recovery_alpha_slow" value="0.0"/>：默认0（MCL），我的0.001。
• <param name="recovery_alpha_fast" value="0.0"/>：默认0（MCL），我的0.8。
• 在rviz里通过2D Pose Estimate按钮移动机器人来触发，机器人位置突变后要过一会儿才注入随机粒子，因为概率是渐变的。

KLD：

• <param name="kld_z" value="0.99"/>： KLD采样以概率$1-\delta（kld_z）$确定样本数。
• <param name="kld_err" value="0.05"/>： 真实的后验与基于采样的近似之间的误差。

动态障碍物：环境中的动态物体总是会获得比静态障碍物更短的读数，因此可以根据这样的不对称性去除异常值。

• 静态障碍物应该服从稳定的高斯分布，以距离传感器的真实距离为均值。
• 扫描到动态目标的beam则服从衰减分布，$-\eta e ^{-\lambda z}$。
• laser_model_type：使用beam model时会用到四个混合权重参数z_hit，z_short，z_max和z_rand，使用likelihood_field model时使用两个z_hit和z_rand。
  • laser_z_hit：default=0.95，以真实值为均值的噪声高斯分布
  • laser_z_rand：defualt=0.05，随机测量权重，均匀分布
  • laser_z_short：default=0.1，意外对象权重，衰减分布
  • laser_z_max：default=0.05，测量失败权重，0/1分布

初始位姿：

• 可以在rviz里通过2D Pose Estimate按钮设定（rviz会发布initialPose话题）。

• 或者写在launch文件中：

  <param name="initial_pose_x"            value="0.0"/>
  <param name="initial_pose_y"            value="0.0"/>
  <param name="initial_pose_a"            value="0.0"/>      
  <param name="initial_cov_xx"            value="0.25"/>
  <param name="initial_cov_yy"            value="0.25"/>
  <param name="initial_cov_aa"            value="(pi/12)*(pi/12)"/>

• 调用全局定位服务：

  rosservice call /global_localization "{}"

  位姿随机初始化，粒子洒满地图：

  

transform_tolerance：

• 默认是0.1seconds，官方定义是Time with which to post-date the transform that is published, to indicate that this transform is valid into the future. tf变换发布推迟的时间，意思是tf变换在未来这段时间内是可用的。
• 【存疑】我个人理解tf的更新频率应该越快越准确，launch文件中最开始设定为0.5，但是实际上机器人移动速度调快时，会报错Costmap2DROS transform timeout...Could not get robot pose, cancelling reconfiguration，然后我调整为1.5就不报错了。
• 目前设定为1.0，仿真里观测不出差异。