A-star algorithm

发表于 |

有目的性地寻找最佳路径，首先定义一个损失函数，表示节点消耗：

$g$表示起点到当前节点的已知消耗

$h$表示对当前节点到终点消耗的猜测，估价函数有多种形式——启发式探索的核心

算法流程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
初始化openList
初始化closeList
将起点放入openList
while openList非空：
	找到开启列表上f最小的节点，记为q
    找到q周围的子节点p，记其父节点为q
    for 每一个子节点p：
    	if p是终点：
        	算法终止
            
        p.g = q.g + qp
        p.h = h(p, terminate)
        p.f = p.g + p.h
        if p已经在开启列表中且保存的f值小于当前计算值||p在关闭列表中：
        	跳过该节点
		else：
        	if p已经在开启列表中：
        		修改该节点的信息（父节点、fgh）
			else：
            	将该节点加入openList
	将q放入closeList

算法性能在细节上的优化：http://theory.stanford.edu/~amitp/GameProgramming/

序言：路径搜索算法的前世今生

Dijkstra算法：从初始节点开始向外扩展，直到到达目标节点。算法保证能找到从初始点到目标点的最短路径。

最佳优先搜索BFS算法：算法能够评估任意节点到目标点的代价，并优先选择离目标最近的结点。启发式算法，比Dijkstra算法运行快得多，但是不能保证路径最短。

如下面这种情况：

D1 B1

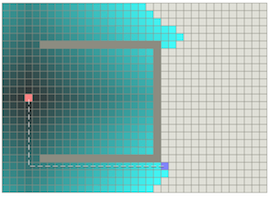
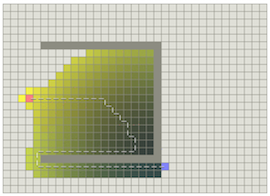
因为BFS是基于贪心策略的，它只关注到尽可能向着目标点移动，而不考虑已花费的代价。Dijkstra算法则正相反，它会确保每一步都是最优的，但是为此要遍历周围全部的节点。

A*算法：将两种路径搜索算法的思想结合起来，考虑两个极端及其中间的情况：

  • 如果$h(n)$是0，只有$g(n)$起作用，那么算法演变为Dijkstra算法。

  • 如果$h(n)$能够始终满足“比当前节点移动到目标节点的实际代价小”，那么算法保证能够找到最短路径。（$h(n)$越小，算法扩展的节点数就越多）

  • 如果$h(n)$能够精确等于“当前节点移动到目标节点的实际代价”，那么算法将会仅仅扩展最优路径。而不扩展其他节点，算法运行非常快。
  • 如果$h(n)$有时会“比当前节点移动到目标节点的实际代价大”，那么此时算法不能保证最短路径了。
  • 如果$g(n)$比$h(n)$小的多，只有$h(n)$起作用，那么算法演变为BFS算法。

估价函数Heuristic function $h(a, b)$

估价函数的选择可以follow以下的instructions：

  1. square grid that allows 4 directions：use Manhattan distance (L1)

  2. square grid that allows 8 directions：use Diagonal distance (L∞)

    当$D = D2 =1$时，$dis = dx + dy -min(dx, dy) = max(dx, dy)$，这个距离称为切比雪夫距离。

    当$D = 1, D2 =\sqrt 2$时，这个距离称为octile distance。

  3. square grid that allows any direcitons：use Euclidean distance (L2)

    If A* is finding paths on the grid but you are allowing movement not on the grid, you may want to consider other representations of the map

    ​ 欧几里得距离并不适用于栅格地图，因为这会导致代价函数g和估价函数的不匹配（代价函数并不是连续的）。

    由于欧几里得距离引入了开根号计算，一些算法会直接用$dis = D(dxdx + dydy)$来代替，*不建议！，会引入尺度问题，$f = g + h$，其中代价函数会逐渐增长，估价函数则逐渐减小，平方会导致两个函数的变化速率不match，使得估价函数的权重过大，导致BFS。

code：

1
2
3
4
5
6
7
8
9
10
11
12
13
public function manhattanHeuristic(a:Object, b:Object):Number {
	return graph.distance(a, b) + simpleCost(a, b) - 1;
}

public function simpleCost(a:Object, b:Object):Number {
	var c:Number = costs[graph.nodeToString(b)];
	if (isNaN(c)) {
		return 1;
	} else {
    	return c;
	}
}
// simpleCost限定为小于等于1的数

此时$h(a,b) = dis(a,b)+c-1 \leq h^{*}(a,b)$，此时能够找到最优解。