一个栗子:整数规划问题欲求$max\ z = 5x_1 + 8x_2$
根据方程组可以绘制下图:
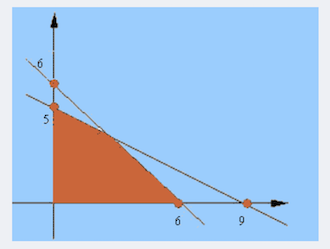
于是可以得到实数空间上的最优解:$x_1 = 2.25, x_2 = 3.75, z_0 = 41.25$。——松弛问题
由于存在整数限定条件:
- 最优解$0 \leq z^{*} \leq 41$,且必为整数
- x_2的最优解不在3和4之间,因为限定为整数
一、分支
于是问题可以拆分为:$max\ z = 5x_1 + 8x_2$
问题拆分的实质是将$x_2$在3和4之间的小数部分划掉了,将可行域拆分成$x_2 \leq 3$ 和$x_3 \geq 4$,但是没有排除任何整数可行解。——分支
二、定界
子问题$p1$的最优解为:$x_1 = 3, x_2=3, z^{*}=39$
子问题$p2$的最优解为:$x_1 = 1.8, x_2=4, z^{*}=41$
也就是说,子问题$p1$的整个参数空间上,能够取得的最优解为39,子问题$p2$上则为41,显然最优解应该位于子问题$p2$所在的参数空间中,且$39\leq z^{} \leq41$。——*定界
三、迭代
对$p2$参数空间再分支,参数$x_1$可以拆分为$x_1 \leq 1$和$x_1 \geq 2$:
四、总结
分支定界算法的总体流程如下:
- 先求解相应的松弛问题,得到最优解,检查其是否符合原问题约束,若符合则为最优解,否则进行下一步。
- 定界,取各分支中目标函数最大的作为上界$U_z$,取其余分支中目标函数中最大的作为下界$L_z$。$L_z \leq z^{*} \leq U_z$。
- 分支,否则选择一个不符合原问题条件的变量,构建子问题。
- 对各分支,有序地,进行步骤1。
在求解对应的松弛问题时,通常会有以下几种情况:
- 松弛问题没有可行解,那么原问题也没有可行解。
- 松弛问题的最优解也满足原问题约束,那么该解也是原问题的最优解,算法终止。
- 松弛问题的最优解小于现有下界,那么应该对该子问题进行剪枝。
五、DFS
对一颗搜索树,不用计算每一层全部节点的score(BFS),我们会维护一个优先队列,其中按照score的大小存放节点,然后选择score最大的节点(the most promising child)进行分支。