skid-steer drive

实验中使用了两种类型的底盘，基于差速驱动的2WD底盘和基于滑动转向的4WD底盘。两种驱动方式原理相似，也有其显著的区别。

相同点：

两种底盘都没有显示的转动机制，采用差速驱动的方式通过以不同的方向或速度驱动两边轮子来实现方向控制。

差速驱动的运动形式通常有一下几种类型：

• 第一种是原地旋转，左右轮的速度大小相等，方向相反，这样相当于绕着底盘的形心原地打转。
• 第二种是沿着某个方向直线行走，此时左右轮速度相同。
• 第三种是沿着某条曲线前行或后退，此时左右轮速度方向相同，大小不同。
• 第四种是旋转转弯，此时左右轮速度方向相反。

两种机构共同的优势是：没有显示的转向机构，极大地简化了运动学模型。

而两种机构共同的缺点是：由于两侧的轮子是由独立电机分别驱动的，直线运动要求两侧的轮子以相同速度转动，这将很难完成。

不同点：

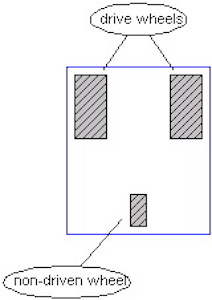
差速驱动底盘通常是由一个两轮系统，每个轮子都带有独立的执行机构（直流电机），以及一个无驱动轮（可以是脚轮或者万向滚珠）组成，机器人的运动矢量是每个独立车轮运动的总和。

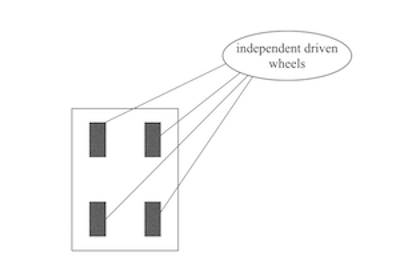
滑动转向底盘通常被用在履带车上，比如坦克和推土机，也被用于某些四轮六轮机构上，相比较于两轮差速底盘，滑动转向的主要区别在于：

• 优势：滑动转向使用了两个额外的驱动轮代替了差速驱动的脚轮，增大了牵引力。
• 劣势：引入了滑动，在对里程计要求高的场景中，滑动是一个致命的缺陷，因为这会对编码器造成负面影响，滑动的轮子不会跟踪机器人的确切运动。

运动学分析：

对于差速驱动机构，移动机器人航向角变化了多少角度，它就绕其运动轨迹的圆心旋转了多少角度。这句话很好验证，我们让机器人做圆周运动，从起点出发绕圆心一圈回到起点处，在这过程中机器人累计的航向角为360度，同时它也确实绕轨迹圆心运动了360度。

机器人的速度是指两个相邻的控制时刻之间的速度，因此小车的行驶轨迹可以分解为连续的圆弧片段，对于每一段圆弧，根据阿克曼转向几何原理，在小车转向时，为保证行驶稳定性，两侧轮胎都近似围绕一个中心点旋转。即整个小车底盘都围绕一个中心点旋转，已知小车中心的线速度（上层算法给定），此时小车底盘的运动学模型如下图：

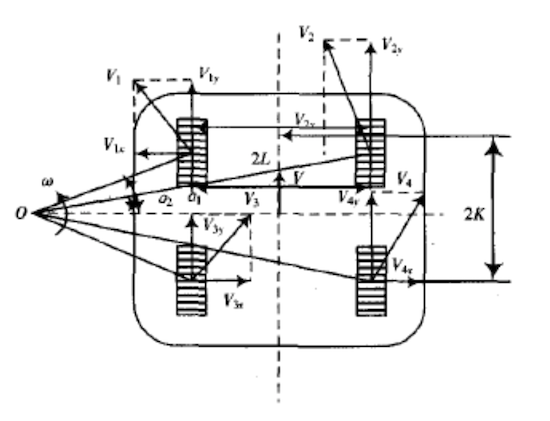
参数说明：

$\alpha_1$是小车前左轮和后左轮的转角。

$\alpha_2$是小车前右轮和后右轮的转角。

$2L$是左右轮距离。

$2K$是前后轮距离。

$w$是小车转轴的角速度。

$v$是小车几何中心的线速度。

$v1, v2, v3, v4$是四个车轮的速度。

$i$是电机的减速比。

$r$是车轮半径。

首先可以得到各车轮速度和角速度的关系：

$$V_1 = w * R_1 = w * \frac{K}{sin\alpha_1}\\ V_2 = w * R_2 = w * \frac{K}{sin\alpha_2}\\ V_3 = V_1 = w * \frac{K}{sin\alpha_1}\\ V_4 = V_2 = w * \frac{K}{sin\alpha_2}\\$$

其中车轮沿着转动方向（$y$方向）的速度由电机提供，切向速度由地面摩擦提供，车轮沿着$y$方向的速度为：

$$R =\frac{v}{w}\\ V_{1y} = V_1 * cos\alpha_1 = w * \frac{K}{tan \alpha_1} = w(R-L)\\ V_{2y} = V_2 * cos\alpha_2 = w * \frac{K}{tan \alpha_2} = w(R+L)\\ V_{3y} = V_{1y} = w(R-L)\\ V_{4y} = V_{2y} = w(R+L)\\$$

那么电机的角速度为：

$$w_n= \frac{V_{ny}*i}{r}, n = 1,2,3,4\\$$

相应电机的转速（by rpm）为：

$$n = \frac{w_n*60}{2\pi}$$

整理成矩阵表达式为：

$$\begin{bmatrix} w_1\\ w_2\\ w_3\\ w_4 \end{bmatrix}= \begin{bmatrix} 1 & - L\\ 1 & L\\ 1 & - L\\ 1 & L \end{bmatrix} \begin{bmatrix} v\\ w \end{bmatrix}$$

该表达式反映了机器人关键点速度与主动轮转速之间的关系。给定小车底盘电机转速就可以求出机器人关键点的速度，并由此得到机器人上任意一点的速度（如激光雷达的安装位置的速度），上层算法给出的关键点速度控制信号也可以由此转化成电机的控制量。

里程计模型 ／ 机器人定位方法

坐标变换模型：

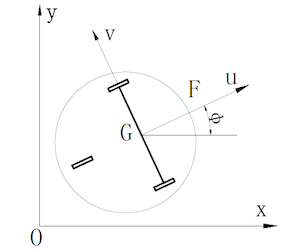
在一个较短的时间间隔$\Delta t$内，假定机器人左右轮的移动距离分别是$\Delta l$和$\Delta r$，那么在机器人坐标系下：机器人中心沿着机器人坐标系的$x$轴方向前进的距离为$\Delta u = (\Delta l + \Delta r)/2$，$y$轴方向前进的距离为$\Delta v = 0$，转过的角度为$\Delta \varphi = (\Delta l - \Delta r)/b$。机器人坐标系到世界坐标系的旋转变换矩阵为$R(\phi)$。

那么转换到世界坐标系下机器人的运动增量为：

$$\begin{bmatrix} \Delta x\\ \Delta y\\ \Delta \phi \end{bmatrix} = \begin{bmatrix} R(\phi) & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} \Delta u\\ \Delta v\\ \Delta \varphi \end{bmatrix} = \begin{bmatrix} cos\phi & sin\phi & 0\\ -sin\phi & cos\phi & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} (\Delta l + \Delta r)/2\\ 0\\ (\Delta l - \Delta r)/b \end{bmatrix}$$

世界坐标系下机器人位姿更新为：

$$\begin{bmatrix} x_t\\ y_t\\ \phi_t \end{bmatrix} = \begin{bmatrix} cos\phi_{t-1}(\Delta l + \Delta r)/2\\ sin\phi_{t-1}(\Delta l + \Delta r)/2\\ (\Delta l - \Delta r)/b \end{bmatrix} + \begin{bmatrix} x_{t-1}\\ y_{t-1}\\ \phi_{t-1} \end{bmatrix}$$

beside from测量误差，利用坐标变换模型去推算里程计信息是引入了模型误差的——在时间间隔$\Delta t$内，为了简化计算，机器人坐标系相对世界坐标系的旋转变换矩阵被假定为起始值$R(\phi)$。在转向运动比较多的情况下，里程计信息会迅速恶化。

圆弧模型：

将极小时间间隔内小车运动的轨迹看作是一段圆弧，那么就可以确定该时刻的转动中心$C_{t-1}$，及内侧轮的转动半径为$R_{t-1}$，根据几何关系：

$$\left\{ \begin{align} &\Delta l = (b + R)\Delta \varphi\\ &\Delta r = R \Delta \varphi \end{align} \right.$$

解得：

$$\left\{ \begin{align} &R = \frac{b\Delta r}{\Delta l - \Delta r}\\ &\Delta \varphi = \frac{\Delta l - \Delta r }{b} \end{align} \right.$$

由三角相似得：

$$\frac{Rsin(\Delta \varphi/2)}{D/2} = \frac{R}{R + b/2}$$

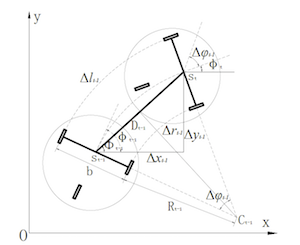
解得弦$D$的长度为：

$$D = [b(\Delta l + \Delta r)/(\Delta l-\Delta r)]sin[(\Delta l - \Delta r)/2b]$$

弦$D$与世界坐标系$x$轴正向的夹角为$\theta = \phi - \Delta \varphi/2$，那么机器人在世界坐标系下的位姿增量为：

$$\left\{ \begin{align} &\Delta x_{t-1} = D_{t-1} cos\theta_{t-1}\\ &\Delta y_{t-1} = D_{t-1} sin\theta_{t-1}\\ &\Delta \varphi = (\Delta l - \Delta r )/b \end{align} \right.$$

使用圆弧模型对里程计增量进行推算，完全依照几何关系来计算，计算过程中没有近似，能够有效控制误差累积。

概率模型：

不是单纯的基于里程计的估计，而是结合其他传感器的测量值对里程计进行矫正，详见滤波算法。

scan match模型：

同样也不是单纯的基于里程计的估计，详见karto scanMatch。与滤波的区别在于，返回的不是概率分布，而是一个代表最佳估计的值。