状态估计

1. 概述

• 经典的SLAM模型由一个运动方程和一个观测方程构成： $$\left\{ \begin{split} & x_k = f(x_{k-1}, u_k) + w_k\\ & z_{k,j} = h(y_i, x_k) + v_{kj} \end{split} \right.$$ 其中，$x_k$表示相机的位姿，可以用变换矩阵或李代数来表示，$y_i$表示路标，也就是图像中的特征点，$w_k$和$v_{kj}$表示噪声项，假设满足零均值的高斯分布。

• 我们希望通过带噪声的观测数据$z$和输入数据$u$推断位姿$x$和地图$y$的概率分布。主要采用两大类方法，一类是滤波方法：基于当前状态来估计下一状态，忽略历史；一类是非线性优化方法，使用所有时刻的数据估计新状态的最优分布。
  • 滤波方法主要分为扩展卡尔曼滤波和粒子滤波两大类。
  • 非线性优化根据实现细节的不同主要分为滑动窗口法和Pose Graph法。

2. 非线性优化

• 非线性优化基于历史，同时也作用于历史，因此把所有待估计的变量放在一个状态变量中：

  $$x = \{x_1, ..., x_N, y_1, ..., y_M\}$$

  在已知观测数据$z$和输入数据$u$的条件下，对机器人的状态估计：

  $$P(x | z,u)$$

  先忽略测量运动的传感器，仅考虑测量方程，根据贝叶斯法则：

  $$P(x|z) = \frac{P(z|x)P(x)}{P(z)} \varpropto P(z|x)P(x)$$
  • 先验概率$P(x)$：先验的概念最好理解，就是一个事件的概率分布。
  • 似然概率$P(z|x)$：已知事件的概率分布，事件中某状态的概率。
  • 后验概率$P(x|z)$：在给定数据条件下，不确定性的条件分布。
  • $Posterior \varpropto Likelihood * Prior$

  求解后验分布比较困难，但是求一个状态最优估计（使得后验概率最大化）是可行的：

  $$x^*_{MAP} = argmaxP(x|z) = argmaxP(z|x)P(x) = argmaxP(z|x)$$

  因为先验概率不知道，所以问题直接转成为求解极大似然估计，问题中的未知数是$x$，直观意义就是：寻找一个最优的状态分布，使其最可能产生当前观测到的数据。

• 假设了噪声项$v_{kj} \thicksim N(0, Q_{k,j})$，所以极大似然概率也服从一个高斯分布：

  $$P(z_{kj}|x_k, y_j) = N(h (y_j, x_i), Q)$$

  求高斯分布的最值通常取负对数处理，最大化变成求最小化：

  $$P(x) = \frac{1}{\sqrt{(2\pi)^Ndet(\Sigma)}} exp\bigg(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\bigg)\\ -ln(P(x) ) = \frac{1}{2}ln\big((2\pi)^Ndet(\Sigma)\big) + \frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)$$

  对数第一项与$x$无关，第二项等价于噪声的平方项。因此可以得到优化问题的目标函数：

  $$e_{k} = x_k - f(x_{k-1}, u_k)\\ e_{kj} = z_{kj} - h(x_k, y_j)\\ J(x) = \Sigma e_k^TR^{-1}_ke_{k} + \Sigma e_{kj}^TQ^{-1}_ke_{kj}\\ x* = argmin_x J(x)$$

  以上的最小二乘问题可以采用各种各样的梯度下降法求解最优解（参考图优化）。

• Bundle Ajustment

  优化问题最终可以表示成$H\Delta x = g$的形式，其对角线上的两个矩阵为稀疏矩阵，且右下角的矩阵维度往往远大于左上角（因为特征点的数目远大于位姿节点）：

  $$H = \begin{bmatrix} B &E\\ E^T & C \end{bmatrix}$$

  一个有效的求解方式称为Schur消元，也叫边缘化Marginalization，主要思路如下：首先求解$C$矩阵的逆矩阵，然后对$H$矩阵进行消元，目标是消去其右上角的$E$矩阵，这样就能够先独立求解相机参数$\Delta x_c$，再利用求得的解来求landmarks参数$\Delta x_p$：

  $$\begin{bmatrix} I &-EC^{-1}\\ 0 & I \end{bmatrix} \begin{bmatrix} B &E\\ E^T & C \end{bmatrix} \begin{bmatrix} \Delta x_c \\ \Delta x_p \end{bmatrix} = \begin{bmatrix} I &-EC^{-1}\\ 0 & I \end{bmatrix} \begin{bmatrix} v \\ w \end{bmatrix} \\ \begin{bmatrix} B - EC^{-1}E^T & 0\\ E^T & C \end{bmatrix}\begin{bmatrix} \Delta x_c \\ \Delta x_p \end{bmatrix} = \begin{bmatrix} v - EC^{-1}w\\ w \end{bmatrix}$$

  因此可以解得$\Delta x_c$：

  $$\begin{bmatrix} B - EC^{-1}E^T \end{bmatrix} \Delta x_c = v - EC^{-1}w$$
  • 这个矩阵称为消元之后的$S$矩阵，它的维度与相机参数的维度一致
  • $S$矩阵的意义是两个相机变量之间是否存在着共同观测点
  • $S$矩阵的稀疏性由实际数据情况决定，因此只能通过普通的矩阵分解的方式来求解

• 核函数

  当误差很大时，二范数增长的很快，为了防止其过大掩盖掉其他的边，可以将其替换成增长没那么快的函数，使得整个优化结果更为稳健，因此又叫鲁棒核函数，常用的核有Huber核、Cauchy核、Tukey核等，Huber核的定义如下：

  $$H(e) = \left\{ \begin{split} & \frac{1}{2} e ^2, \ \ \ |e| \leq \delta\\ & \delta(|e| - \frac{1}{2}\delta), \ \ else \end{split} \right.$$

3. 卡尔曼滤波

滤波思路基于一个重要的假设：一阶马尔可夫性——k时刻状态只与k-1时刻状态有关，整理成两个要素如下：

• $x_{k-1}$ contains the whole history
• $x_k = f(x_{k-1}, u_k, z_k)$

在这里我们只需要维护一个状态量$x_k$，并对它不断进行迭代更新，moreover，如果状态量服从高斯分布，我们只需要维护状态量的均值和方差即可（进一步简化）。

首先考虑一个线性系统：

$$\left\{ \begin{split} & x_k = A_k x_{k-1}+u_k + w_k\\ & z_k = C_k x_k + v_k \end{split} \right.\\ w_k \thicksim N(0, R), v_k \thicksim N(0, Q)$$

卡尔曼滤波器的第一步预测，通过运动方程确定$x_k$的先验分布，注意用不同的上标区分不同的概率分布：尖帽子$\hat x_k$表示后验，平帽子$\bar x_k$表示先验：

$$P(\bar x_k) = N(\bar x_k, \bar P_k)\\ \bar x_k = A_k \hat x_{k-1} + u_k\\ \bar P_k = A_k\hat P_{k-1}A_k^T+R$$

第二步为观测，通过分析实际观测值，计算在某状态下应该产生怎样的分布：

$$P(z_k|x_k) = N(C_kx_k, Q)$$

第三步为更新，根据第一节中的贝叶斯法则，得到$x_k$的后验分布：

$$(\hat x_k, \hat P_k) = N(C_kx_k, Q)N(\bar x_k, \bar P_k)\\ K = \bar P_k C_k^T(C_k\bar P_k C_k^T + Q_k)^{-1}\\ \hat x_k = \bar x_k + K(z_k-C_k\bar x_k)\\ \hat P_k = (I - KC_k)\bar P_k$$

整体的流程图如下：

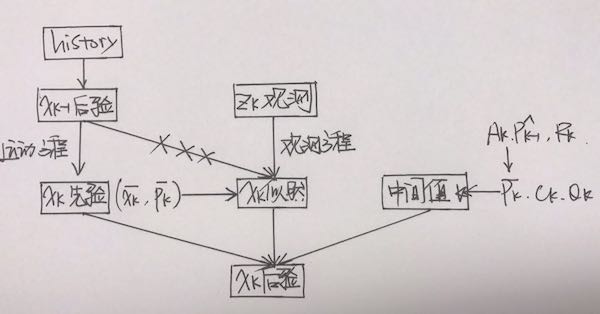
具体过程本节中不做展开，详情可以参考卡尔曼滤波。高斯分布经过线性变换仍然服从高斯分布，因此整个过程没有发生任何的近似，因此可以说卡尔曼滤波器构成了线性系统的最优无偏估计。

下面考虑非线性系统：

SLAM中不管是三维还是平面刚体运动，因为都引入了旋转，因此其运动方程和观测方程都是非线性函数。一个高斯分布，经过非线性变换，通常就不再服从高斯分布，因此对于非线性系统，必须采取一定的近似，将一个非高斯分布近似成高斯分布。

通常的做法是，将k时刻的运动方程和观测方程在$\hat x_{k-1}$，$\hat P_{k-1}$处做一阶泰勒展开，得到两个雅可比矩阵：

$$F = \frac{\partial f}{\partial x_{k-1}}\bigg|_{\hat x_{k-1}}\\ H = \frac{\partial h}{\partial x_k}\bigg|_{\hat x_k}$$

中间量卡尔曼增益$K_k$：

$$\bar P_k = F\hat P_{k-1}F^T + R_k\\ K_k = \bar P_k H^T(H \bar P_k H^T + Q_k)^{-1}$$

后验概率：

$$\hat x_k = \bar x_k + K_k(z_k - h(\bar x_k))\\ \hat P_k = (I - K_k H)\bar P_k$$

对于SLAM这种非线性的情况，EKF给出的是单次线性近似下的最大后验估计（MAP）。

4. EKF VS Graph-Optimization

1. 马尔可夫性抛弃了更久之前的状态，优化方法则运用了更多的信息。
2. 非线性误差：两种方法都使用了线性化近似，EKF只在$x_{k-1}$处做了一次线性化，图优化法则在每一次迭代更新时都对新的状态点做泰勒展开，其线性化的模型更接近原始非线性模型。
3. 存储：EKF维护的是状态的均值和方差，存储量与状态维度成平方增长，图优化存储的是每个状态点的位姿，存储线性增长。