前面说完了 PnP,趁热打铁更新直接法,因为两者的思路基本一致,主要的差别在于PnP中利用的是特征点的重投影误差——匹配点在query帧像素平面上的实际位置和估计位置的误差,直接法不提取特征点,而是采用像素亮度误差。
1. 直接法的推导
以第一个相机为参考系,第二个相机的运动参数为$R, t, \xi$,对某个空间点$P$:
两个像素点的亮度误差:
目标函数:
误差函数关于优化变量的导数:
上面的扰动相关项中,记:
误差函数线性化:
$q$表示扰动分量在第二相机坐标系下的坐标(回顾关于$R$的微分方程:$\dot R(t) = \phi_0^{\wedge}R(t)$),因此$u$的意义为像素坐标,$\frac{\partial I_2}{\partial u}$的物理意义为像素梯度,$\frac{\partial u}{\partial q}$的物理意义为像素坐标关于三维点的导数(参考针孔相机模型),$\frac{\partial q}{\partial \delta \xi}$的物理意义为三维点关于扰动的导数(参考李代数)。
2. 直接法分类
根据P的来源,直接法分为三类:
- P来自于稀疏关键点——稀疏直接法
- P来自部分像素,只使用带有梯度的像素点——半稠密直接法
- P为所有像素——稠密直接法
3. 代码实现
主要关注Edge类里面重定义的增量更新函数linearizeOplus()里面Jacobian矩阵的写法。
- 前一项是$u$处的像素梯度,使用数值导数:
1 | // jacobian from I to u (1*2) |
getPixelValue这个函数涉及到一个双线性插值,因为上面的二维坐标uv是通过相机投影变换得到的,是浮点形式,而像素值是离散的整数值,为了更精细地表示像素亮度,要对图像进行进行插值。
- 线性插值:已知数据$(x_0, y_0)$和$(x_1, y_1)$,要计算$[x_0, x_1]$区间内任一$x$对应的$y$值:
双线性插值:本质上就是在两个方向上做线性插值:
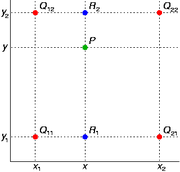
首先是x方向:
然后y方向:
综合起来就是:
1 | inline float getPixelValue ( float x, float y ) |
- 后两项都是与相机参数和三维点坐标有关,可以合并,同时注意g2o中对SE3的定义平移和旋转和本文设定是反过来的。
1 | // jacobian from u to xi (2*6) |