leetcode

lc79

挂一道很猥琐的题，二维网格中搜索单词，同一单元格不能重复使用：

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

给定 word = "ABCCED", 返回 true.
给定 word = "SEE", 返回 true.
给定 word = "ABCB", 返回 false.

没啥好算法，就是DFS，但是坑在于visited的存储，python数组默认浅拷贝，递归传进去再回到上一层网格状态就变了，之前一贯的做法就是新开一块内存空间，传新的数组进去，然而这次超时了，因为测试用例的二维数组尺寸贼大，终于有机会正视这个问题，并获取正确的打开方式：

尺寸贼大的二维数组，每次只需要修改一个值，重新划空间拷贝再修改时间复杂度瞬间增大O(m*n)倍，很明显传原来的数组进去比较合适。

但是深层递归会修改传进去的参数，因此在每次递归之前先创建一个tmp，记录修改行为，递归函数进行完以后，再根据记录恢复原来的参数，保证本层参数不变。

def search_tail(board, word, h, w):
    size = len(word)
    char = word[0]
    height, width = len(board), len(board[0])
    exist = False
    if h - 1 >= 0 and board[h-1][w] == char:
        if size == 1:
            return True
        else:
            tmp = board[h-1][w]
            board[h-1][w] = 'INF'
            exist = search_tail(board, word[1:], h-1, w)
            if exist:
				return True
            board[h-1][w] = tmp
    if h + 1 < height and board[h+1][w] == char:
        ...
        ...

然后针对本题还有一个骚操作，很多人专门创建一个visited表来记录搜索路径，但是因为本题的二维数组限定存储字母，所以任意一个非字母都可以作为标志位，美滋滋又省下一个O(m*n)。

lc81

实名diss这道题，一看是旋转排序数组直接做了，然后才发现测试样例里面出现了左右边界重合的情况，然后仔细再审题才发现这行小字：

这是搜索旋转排序数组的延伸题目，本题中nums可能包含重复元素

不包含重复元素的情况下代码实现如下：

class Solution:
    def search(self, nums, target):

        size = len(nums)
        start = 0
        end = size - 1
        while start <= end:

            mid = (start + end) // 2
            if nums[mid] == target:
                return True

            if nums[mid] <= nums[end]:
                if target < nums[mid] or target > nums[end]:
                    end = mid - 1
                else:
                    start = mid + 1

            else:
                if target > nums[mid] or target < nums[start]:
                    start = mid + 1
                else:
                    end = mid - 1

        return False

因为数组中现在存在重复的元素，因此有一个特殊的情况：左右边界值相同，并且nums[mid]值与边界值也相同，这时nums[mid]可能位于两段数组的任意一边。因此要独立讨论一下这个情况：

class Solution:
    def search(self, nums, target):

        size = len(nums)
        start = 0
        end = size - 1
        while start <= end:

            mid = (start + end) // 2
            if nums[mid] == target:
            	return True

            if nums[mid] < nums[end]:
            if target < nums[mid] or target > nums[end]:
                end = mid - 1
            else:
                start = mid + 1

            elif nums[mid] > nums[end]:
                if target > nums[mid] or target < nums[start]:
                    start = mid + 1
                else:
                    end = mid - 1

            # nums[mid] = nums[end]的情况
            else:
            	end -= 1
		
        return False

测试用时50ms，因为边界重复的循环没有有效地二分数组，但是思路贼简单啊。

lc95

96和95都是二叉搜索树，先做的96，求树的结构有几种，没注意结点大小关系，用动态规划来做，$dp[i] = dp[0]dp[i-1] + … + dp[i-1]dp[0]$。注意递归调用的时间复杂度，自底向上来算：

def numTrees(self, n):
	res = [1, 1]
    if n < 2:
        return res[n]
    
    res += [0]*(n-1)
    for i in range(2, n+1):
        for j in range(i):
            res[i] += res[j]*res[i-1-j]
	
    return res[n]

95要列出结构了，才发现什么是二叉搜索树来着——左子树的结点值均小于根节点，右子树的结点值均大于根节点。按照惯例，求数量用DP，求枚举则用DFS：

遍历每一个数字$i$作为根节点，那么$[1, 2, …, i-1]$构成其左子树，$[i+1, i+2, …, n]$构成其右子树。

def generateTrees(self, n):
	if n == 0:
        return []
    return self.dfs(1,n)


def dfs(self, b, e):
    if b > e:
        return [None]
    res = []
    for i in range(b, e+1):
        # set as the root node
        leftTrees = self.dfs(b, i-1)
        rightTrees = self.dfs(i+1, e)
        for left in leftTrees:
            for right in rightTrees:
                root = TreeNode(i)
                root.left = left
                root.right = right
                res.append(root)
	return res

lc28

实现 strStr() 函数。给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

KMP算法，两个难点：

O(m)计算needle中每个子串 needle[:k]的最长前缀
O(n)计算无回溯匹配needle

【先分析第一个：

needle的长度为m，那么维护一个等长的前缀数组next，next[0]=0，首字母没有真正意义的前/后缀

对于子串needle[:i]，首先查看子串needle[:i-1]的前缀长度，j=next[i-1]

如果needle[j]=needle[i]，next[i]=j+1
如果不相等，我们目前有needle[:i-1]的前/后缀，needle[0:j]和needle[i-j:i]，显然needle[:i]的前缀只能是needle[0:j]的前缀子串，最长为needle[0:j-1]，同时它还得是needle[i-j:i]的后缀子串，说白了就是在子串needle[0:j]中要最大匹配前/后缀：迭代j=next[next[i-1]-1]，如果子串没有共享前/后缀就是0

next = [0] * len(needle)
for i in range(1,len(needle)):
	j = next[i-1]
	while j>0 and needle[i]!=needle[j]:
		j = next[j-1]
        
	if needle[i]==needle[j]:
		next[i] = j+1

print('next', next)

【再分析查找阶段，对于给定字符串haystack，暴力解法是从头开始匹配，遇到mismatch就回溯到起始点下一位重新开始匹配，这样的时间复杂度是O(nm)，之所以能够做到无回溯匹配，就是因为有了前缀数组，当我们匹配到needle的一半遇到mismatch了，对于已经匹配上的子串，不需要回溯到起始位置，而是可以从共享前/后缀开始匹配，

needle_idx = 0
for i in range(len(haystack)):
	while needle_idx and haystack[i]!=needle[needle_idx]:
		needle_idx = next[max(0,needle_idx-1)]
	if haystack[i]==needle[needle_idx]:
		needle_idx += 1
	if needle_idx>=len(needle):
		return i-len(needle)+1
return -1

lc215

求无序数组中第k个最大元素，题目里的O(n)比较有迷惑性，本来想保留一个含k个大元素的动态数组，一次遍历，但每次插值要O(klogk)，总体的复杂度是O(nklogk)，整个数组排序的复杂度是O(nlogn)，所以直接排序：

快排

算法：随机挑选一个基点pivot，把所有小于它的数都放在它左边，所有大于它的数都放在它右边，对左右两个partition递归进行上述操作，算法复杂度是O(nlogn)

稳定性：不是稳定排序，每次放置的位置并不是严格有序的

优化：partition的过程是原地的，求第K个数的时候可以early stop，不需要严格排序所有segment

def findKthLargest(self, nums: List[int], k: int) -> int:

    def sort_partition(left, right):

    	if left>=right-1:
    		return

        i, j = left, right-1
        while i<j:
            # pivot at i: move right ptr
            while i<j and nums[i]<=nums[j]:
        		j -= 1
            nums[i], nums[j] = nums[j], nums[i]
            # pivot at j: move left ptr
            while i<j and nums[i]<=nums[j]:
        		i += 1
        	nums[i], nums[j] = nums[j], nums[i]

        # early stop in this case
        if i==len(nums)-k:
        	return nums[i]
        if i>len(nums)-k:
        	sort_partition(left, i)
        else:
        	sort_partition(i+1, right)

    # quick sort
    sort_partition(0, len(nums))
    # return the k-th
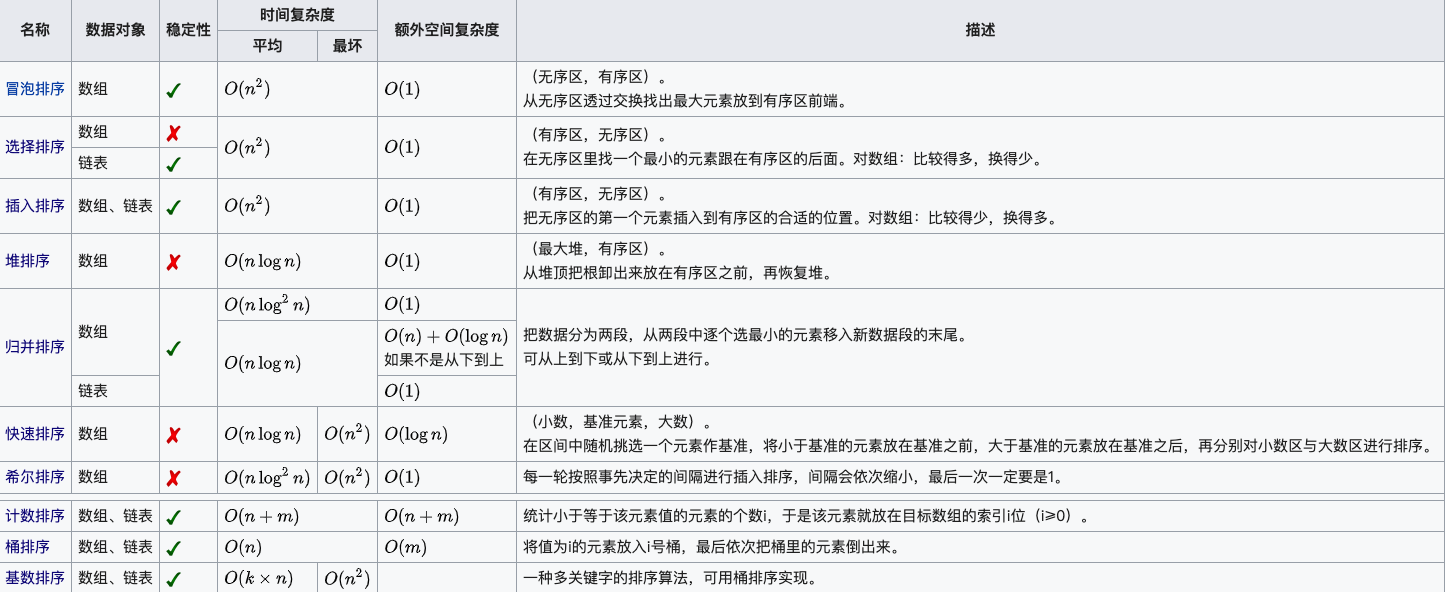
    return nums[-k]

堆排序

堆是完全二叉树：除了最底层之外，每一层都是满的，因此可以推算给定节点的父结点和子结点

given node i：下标从0开始
parent id =(i-1)//2
children id = [2i+1, 2i+2]
最大堆：每个parent node的值都大于其children node
最小堆：每个parent node的值都小于其children node

算法：依次提取堆顶元素，然后重组剩余节点

稳定性：不稳定

给定一个无序数组，如何建立为堆？从队尾开始遍历每个非叶子节点，递归调整树结构

def maxHeapify(lst, i, heap_size):
    left, right = i*2+1, i*2+2
    largest = i
    if left<heap_size and lst[left]>lst[largest]:
        largest = left
    if right<heap_size and lst[right]>lst[largest]:
        largest = right
        if largest!=i:
            # swap
            lst[i], lst[largest] = lst[largest], lst[i]
            maxHeapify(lst, largest, heap_size)

def build(lst):
    # build heap from the last parent node
    n = len(lst)
    for i in range(n//2, -1, -1):
        maxHeapify(lst, i, n)

删除堆顶元素后，如何调整数组成为新堆？用堆尾元素替换堆顶元素，然后逐渐下沉

def heap_sort(lst):
    # take top & ajust the rest
    current_idx = n-1
    while current_idx>0:
        lst[0], lst[current_idx] = lst[current_idx], lst[0]
        maxHeapify(lst, 0, current_idx)
        current_idx -= 1

归并排序

算法：依次合并有序的子序列得到有序数组，有递归和迭代两种实现方式，需要额外的空间来合并子序列，不是原地排序，算法复杂度为O(nlogn)，空间复杂度为O(n)+O(logn)

稳定性：子序列永远升序，是稳定排序
冒泡排序

算法：依次比较相邻元素，如果左>右，就交换，每轮参与比较的最大值会放在最尾部

稳定性：在相邻元素相等时，它们不会交换位置，所以，冒泡排序是稳定排序

优化：early stop，当检测到本轮比较已经没有需要swap的元素时，排序可以提前停止，此时升序数组复杂度为O(n)，倒序数组为O(n^2)
插入排序

算法：维护一个sorted lst和一个unsorted lst，每次从unsorted lst中拿一个元素插入进sorted lst相应位置

稳定性：插入新元素不会打乱已有排序，是稳定排序

优化：查找insert idx时候可以用二分查找减少查找次数，查找次数在logn～n之间，总体的时间复杂度还是O(n^2)