kd-tree

发表于 |

Reference：Bentley J L. Multidimensional Binary Search Trees Used for Associative Searching[J]. Communications of the Acm, 1975, 18(9):509-517.

前面更新basic ICP的时候留了一个坑——最近邻的求法。线性扫描？手动挥手。

1. 先说说距离吧

1.1 欧式距离

1.2 标准化欧式距离

首先将数据各维度分量都标准化到均值为0，方差为1，再求欧式距离：

简单推导后可以发现，标准化欧式距离实际上就是一种加权欧式距离：

1.3 马氏距离（Mahalanobis Distance）

其中$S$为协方差矩阵$Cov$：

若协方差矩阵是单位阵（样本各维度之间独立同分布），那公式就变成欧式距离了，若协方差矩阵是对角阵，那公式就变成标准化欧式距离了。

1.4 相似度

相似度也是距离的一种表征方式，距离越相近，相似度越高。

  • 欧式距离相似度：将欧式距离限定在0 1之间变化
  • 余弦相似度：-1到1之间变化
  • 皮尔逊相关系数：-1到1之间变化
1
return numpy.corrcoef(A, B)

2. KD树

  • k-NN算法
  • 推荐系统
  • SIFT特征匹配
  • ICP迭代最近点
  • 最近在做的M3RCM中的堆结构（这个有点牵强，因为不是二叉树）

总之以上这些基于匹配／比较的目的而进行的数据库查找／图像检索，本质上都可以归结为通过距离函数在高维矢量之间的相似性检索问题。

一维向量有二分法查找，对应地高维空间有树形结构便于快速检索。利用树形结构可以省去对大部分数据点的搜索，从而减少检索的计算量。

KD树是一种二叉树，通过不断地用垂直于某坐标轴的超平面将k维空间切分构造而成。

2d

3d

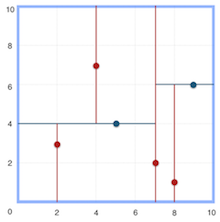
2.1 构造树

递归创建节点：节点信息包含切分坐标轴和切分点，从而确定超平面，将当前空间切分为左右两个子空间，递归直到当前子空间内没有实例为止。

1
2
3
4
5
6
class Node:
	def __init__(self, point, axis):
		self.value = point
		self.axis = axis
		self.left = None
		self.right = None

为了使得构造出的KD树尽可能平衡（高效分割空间）：

  • 选择坐标轴：简单点的方式是循环交替选择坐标轴，复杂点的做法是选择当前方差最大的轴作为切分轴。
  • 选择切分点：取选定坐标轴上数据的中值作为切分点。

注意：KD树的构造旨在高效分割空间，其叶子节点并非是最近邻搜索等应用场景的最优解。

1
2
3
4
5
6
7
8
9
10
def kdTree(points, depth):
	if len(points) == 0:
		return None
	axis = depth % len(points[0])
	points.sort(key=lambda x: x[axis])
	cut_idx = centreValue(points)
	node = Node(points[cut_idx], axis)
	node.left = kdTree(points[:cut_idx], depth+1)
	node.right = kdTree(points[cut_idx+1:], depth+1)
	return node

对于包含n个实例的k维数据来说，构造KD树的时间复杂度为O(k*n*log n)。

2.2 新增节点

递归实现：从根节点开始做比较，大于则插入左子树，小于则插入右子树。直到达到叶子节点，并创建新的叶子节点。

2.3 删除节点

将待删除的节点的所有子节点组成一个集合，重新构建KD子树，替换待删除节点。

2.4 最近邻搜索

搜索最近邻算法主要分为两部分：首先是深度优先遍历，直到遇到叶子节点，生成搜索路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def searchNearest(node, target):
    # input: node: root node of the tree
    #        target: list
    # output: nearest: list
    # 	      dist: distance between target and nearest
    if node == None:
        return None
    # 生成搜索路径
    search_path = deque()
    nearest = node
    print("search path: ")
    while node:
        print(node.value)
        search_path.append(node)
        # if Dist(nearest.value, target) > Dist(node.value, target):
        # 	nearest.value = node.value
        # 	minDist = Dist(node.value, target)

        axis = node.axis
        if target[axis] > node.value[axis]:
            node = node.right
        else:
            node = node.left
    ...
    ...

然后是回溯查找，如果目标点和当前最近点构成的球形区域与其上溯节点相交，那么就有一种潜在的可能——上溯节点的另一个子空间的实例可能位于当前这个球形区域内，因此要进行一次判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def searchNearest(node, target):
    # input: node: root node of the tree
    #        target: list
    # output: nearest: list
    # 	      dist: distance between target and nearest
    ...
    ...
    # 回溯
    print("\nsearch backwards: ")
    nearest = search_path.pop()
    minDist = Dist(nearest.value, target)

    while search_path:
        node = search_path.pop()
        print(node.value)
        if node.axis:
            axis = node.axis
            if minDist > Dist1(node.value[axis], target[axis]):
                if target[axis] > node.value[axis]:
                    search_path.append(node.left)
                else:
                    search_path.append(node.right)
        if Dist(target, nearest.value) > Dist(node.value, target):
            nearest = node
            minDist = Dist(node.value, target)
    return nearest.value, minDist

两个参考点：

1
2
3
samples = [(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)]
target = (2.1, 3.1)
target = (2, 4.5)

KD树搜索的核心就是：当查询点的邻域与分割超平面两侧空间交割时，需要查找另一侧子空间！！！算法平均复杂度O(N logN)。实际时间复杂度与实例分布情况有关，$t_{worst} = O(kN^{1-\frac{1}{k}})$，通常要求数据规模达到$N \geq 2^D$才能达到高效的搜索。

s1

s2

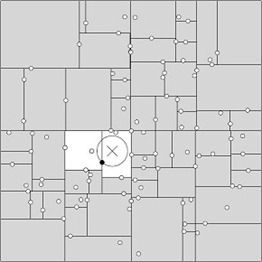
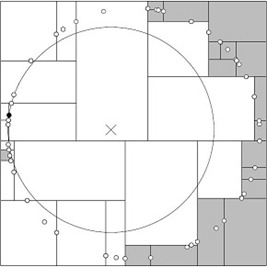
3. 改进算法：BBF算法

回溯是由查询路径决定的，因此一种算法改进思路就是将查询路径上的结点排序，回溯检查总是从优先级最高的树节点开始——Best-Bin-First BBF算法。该算法能确保优先检索包含最邻近点可能性较高的空间。

  • 优先队列：优先级取决于它们离查询点的距离，距离越近，优先级越高，回溯的时候优先遍历。
  • 对回溯可能需要路过的结点加入队列：切分的时候，把未选中的那个兄弟结点加入到队列中。